برای رسم ناحیهٔ تعیینشده بوسیلهٔ شرطها، خیلی راحت بر روی صفحهٔ $x_1\circ x_2$ دو خطِ $2x_1+3x_2=12$ و $2x_1+x_2=8$ را میکشید و با امتحان یک نقطه از هر یک از دو طرف هر کدام از خطها میتوانید تشخیص دهید که کدام سمت را نیاز دارید. شکل حاصل در زیر آمدهاست که ناحیهٔ مورد قبول برای متغیرها با رنگ آبیِ آسمانی پر شدهاست.
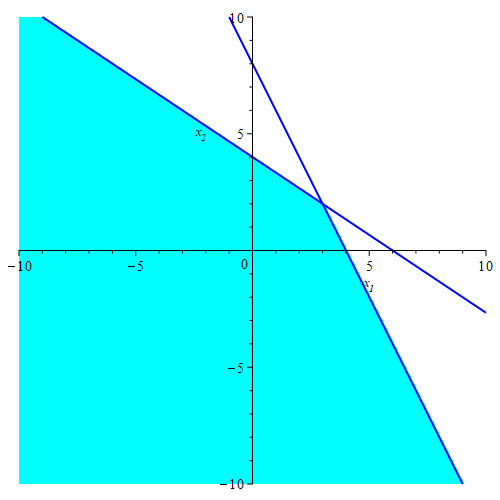
اما برای رسم مقدار تابع $z$ بر روی این ناحیه. توجه کنید که $z=-x_1-\frac{1}{2}x_2$ برابریِ یک صفحه در فضای سهبعدیِ $x_1\circ x_2\circ z$ است. رسم آن کاری ندارد. به هر حال. توجه کنید که نقطهای که گوشهٔ تیز ناحیهٔ بالا بود یک خط عمود بر صفحهٔ $x_1\circ x_2$ تعریف میکند (مختص $z$ آزاد است). اکنون اشتراک یک خط غیر موازی با یک صفحه، با آن صفحه چه میشود؟ یک نقطه. پس مختصات این نقطه را بیابید. نقطه در صفحهٔ متغیرها $(4,0)$ بود (از کجا میدانیم؟ با حل دستگاه دو برابری، دو مجهول خطی تقاطع دو خط). خیلی ساده با جایگذاری در ضابطهٔ $z$ داریم $(4,0,-4)$. پس این نقطه را یافتیم. سپس قسمتی از خط نخست که جزو مرز ناحیه بود را در نظر بگیرید، با مختص $z$ آزاد، این یک نیمصفحه در فضای سهبعدی ایجاد میکند که چون موازی با صفحهٔمان نیست پس آن را در یک خط قطع میکند. برابریِ این خط را هم راحد میتوانید بدست آورید، که در واقع چیزی به جز $2x_1+3x_2=12,z=-x_1-\frac{1}{2}x_2$ نیست. رسم خط در فضای سهبعدی را نیز بلد هستید. به همین شکل برای مرز دوم ناحیه عمل کنید. اینگونه مرز دقیقی که باید از صفحهٔ اصلی برش دهید مشخص است. اکنون خیلی راحت با نگاه به اینکه کدام دو سمت این مرز بالا/پائین ناحیهٔ متغیرها قرار میگیرد میتوانید شکل نمودار را به طور یکتا انتخاب کنید.
اما خیلی راحت هم میتوانستید تنها نقطهٔ گوشه و یک نقطه از هر یک از دو مرز و یک نقطه از داخل ناحیه بردارید و مقدار $z$ را در این چهار نقطه بدست آورید و سپس با وصل کردن و امتداد قسمت صفحهٔ مورد نظر را رسم کنید و همینطور تنها با مقایسهٔ مقدار تابع در این چهار نقطه میتوانید متوجه شوید که کمینه در گوشه رخ میدهد یا در راستای یکی از این دو مرز به منفی بینهایت میرود یا در راستای داخل ناحیه به منفی بینهایت میرود. که در این مثال کمینه در گوشه و یکی از مرزها همزمان رخ میدهد یعنی پرسش بینهایت پاسخ دارد و همهٔ این پاسخها مقدار $-4$ را ایجاد میکنند. شکل سهبعدی در زیر آمدهاست. صفحهٔ اصلی با بنفش و صفحهٔ ناحیهٔ متغیرها با آبی آسمانی رنگ شدهاند.
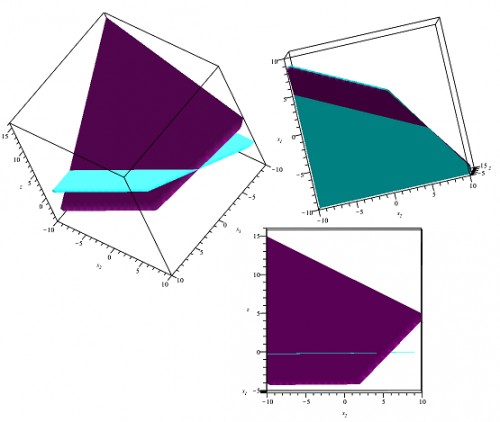
اگر برایتان درک این شکل دشوار است میتوانید از نرمافزار کمک بگیرید که میتوان در آن شکل را چرخاند. برای نمونه در زیر کد ایجاد این شکلها با نرمافزار Maple گذاشتهشدهاست.
شکل دوبعدی:
pline1:=plots:-implicitplot(2*x[1]+3*x[2]=12,x[1]=-10..10,x[2]=-10..10,thickness=2,color=blue):
pline2:=plots:-implicitplot(2*x[1]+x[2]=8,x[1]=-10..10,x[2]=-10..10,thickness=2,color=blue):
fregion:=piecewise(2*x[1]+3*x[2]<=12 and 2*x[1]+x[2]<=8,1,0):
pregion:=plots:-implicitplot(fregion>=1/2,x[1]=-10..10,x[2]=-10..10,filled=true,color=blue,coloring=[cyan,white]):
plots:-display(pregion,pline1,pline2,view=[-10..10,-10..10],scaling=constrained);
شکل سهبعدی:
fregion:=piecewise(2*x[1]+3*x[2]<=12 and 2*x[1]+x[2]<=8,0,undefined):
fz:=piecewise(2*x[1]+3*x[2]<=12 and 2*x[1]+x[2]<=8,-x[1]-x[2]/2,undefined):
pregion3d:=plot3d(fregion,x[1]=-10..10,x[2]=-10..10,color=cyan,style=surface):
pz3d:=plot3d(fz,x[1]=-10..10,x[2]=-10..10,color=purple,style=surface):
plots:-display(pregion3d,pz3d,view=[-10..10,-10..10,-5..16],scaling=constrained,orientation=[0,65,-20],labels=[x__1,x__2,z]);
اگر هم میخواهید پاسخ را چک کنید. میتوانید دستور زیر را برای درخواست از نرمافزار برای یافتن پاسخ مسألهٔ بهینهسازیتان به کار ببرید.
Optimization:-Minimize(-x__1-x__2/2,{2*x__1+3*x__2<=12,2*x__1+x__2<=8});
که به شما خروجیِ $-4$ در نقطهٔ $(4,0)$ را میدهد.