بدترین کاری که یک دانشآموز، دانشجو، شاگرد یا فراگیر ریاضی میتواند انجام دهد این است که پس از خواندن یک پرسش هیچ کاری انجام ندهد! فرض کنیم یک یا چند چیز در این پرسش برای شما مفهوم نیست مثلا اینکه از عدد برای رنگها استفاده شدهاست یا تعریف تابعهای چگالی و انباشتگی یا کشیدن نمودار، آیا اینکه احتمال انتخاب شدن یک توپ آبیرنگ از یک جعبهٔ شامل ۶ توپ سفید، ۳ توپ قرمز و ۱ توپ آبی چقدر است را هم نمیتوانستید محاسبه کنید؟ اگر مشکلتان در زمینهٔ حساب کردن این احتمالها بود که پرسشهای مشابه در سایت هست یا دستکم در متن پرسش اشاره میکردید مشکلتان اینجاست. اگر مشکلتان اینجا نیست پس دست کم دست به مداد میشدید و این یک کار را میکردید و سپس میگفتید فلان مرحلهٔ بعد را چگونه انجام دهم!
شما یک جعبه با ۱۰ توپ دارید. یک توپ را شانسی بیرون میکشید. چند حالت برای رنگ آن وجود دارد؟ ۳ حالت؛ سفید، قرمز و آبی. یک آزمایش با سه برآورد دارید. متغیر تصادفی مربوط به این آزمایش را با $X$ نمایش میدهید و به جای اینکه مقدار رو شده برای این متغیر را با واژهها بنویسید با چند عدد قرارداد میکنید. یعنی به جای نوشتنِ «$X=\text{سفید}$»، مینویسید «$X=1$». به همین سادگی. اکنون برویم به سراغ دو تابع احتمال، یکی چگالی و دیگری انباشتگی. تابع چگالی برای یک متغیر تصادفی گسستهٔ متناهی یعنی احتمال رخ دادن هر یک از اعضای فضای نمونه. شما سه عضو در فضای نمونه دارید ۱ و ۵ و ۱۰ (که همان سفید و قرمز و آبی هستند). احتمال سفید بودن چقدر است؟ ۶ تا از این ۱۰ توپ سفید است پس $\frac{6}{10}$. در نتیجه اگر $P$ برای احتمال و $f_X$ برای تابع چگالی به کار رود میتوانیم بنویسیم؛
$$f_X(1)=P(\lbrace 1\rbrace)=0.6$$
به روش مشابه داریم $f_X(5)=0.3$ و $f_X(10)=0.1$. برای هر $x\not\in\lbrace 1,5,10\rbrace$ نیز $f_X(x)=0$. میتوانید به شکل زیر نیز تابع $f_X$ را بنویسید.
$$f_X(x)=\begin{cases}
0.6 &;\; x=1\\
0.3 &;\; x=5\\
0.1 &;\; x=10\\
0 &;\;\text{otherwise}
\end{cases}$$
واژهٔ otherwise یعنی «در غیر اینصورت». رسم نمودار آن هم ساده است، یک نمودار میلهای دارید! پیشتر برای یک پرسش دیگرتان این نمودار را معرفی کردم و دستور کشیدن آن با نرمافزار Mathematica را هم برایتان گذاشتم. همیشه تلاش کنید از پاسخی که میگیرید یاد بگیرید و مطالب یاد گرفته شده را برای موارد مشابه به کار ببرید! در زیر نمودار تابع چگالی این پرسش را میبینید (به همراه دستور Mathematicaاش).
BarChart[{{6/10,3/10,1/10}},ChartLabels->{1,5,10},ChartStyle->Blue,AxesLabel->{ToExpression["x",TeXForm,HoldForm],ToExpression["f_X(x)",TeXForm,HoldForm]},LabelStyle->Directive[Black,16]]
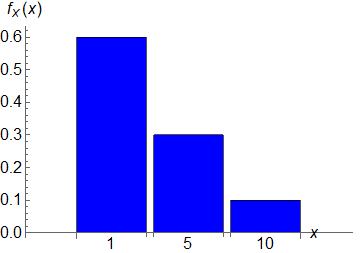
اکنون به سراغ تابع انباشتگی برویم. تنها جایی که ممکن است یک شاگرد معمولی با فرض اینکه دبیر مربوطه تا پیش از اینجا را درست آموزش دادهباشد ممکن است گیج شود، باید اینجا باشد که البته پس از دیدن یک نمونه یا کمی فکر کردن یا راهنمایی باید سردرگمیِ ایجاد شده رفع گردد. تابع انباشتگی را با $F_X$ نمایش دهید. در این صورت تعریفِ آن چه بود؟ تعریف آن به شکل زیر بود.
$$F_X(x)=P((-\infty,x])$$
که چون متغیر تصادفی شما گسسته و متناهی است پس
\begin{align}
F_X(x) &=P((-\infty,x])\\
&=P(\lbrace y\in\lbrace 1,5,10\rbrace\mid y\leq x\rbrace)\\
&=\sum_{\substack{y\leq x\\ y\in\lbrace 1,5,10\rbrace}}P(\lbrace y\rbrace)\\
&=\sum_{\substack{y\leq x\\ y\in\lbrace 1,5,10\rbrace}}f_X(y)
\end{align}
پس برای مثال $F_X(6)$ بعنی احتمال اینکه $X$ عضو $\lbrace 1,5\rbrace$ بیفتد یا به زبان سادهتر توپ بیرون کشیده شده یا سفید باشد یا قرمز. خیلی ساده باید متوجه شوید که چرا ضابطهٔ $F_X$ به شکل زیر درخواهدآمد.
$$F_X(x)=\begin{cases}
0 &;\; x<1\\
0.6 &;\; 1\leq x<5\\
0.9 &;\; 5\leq x<10\\
1 &;\; 10\leq x
\end{cases}$$
نمودار آن را میتوانید میلهای بکشید اگر که محور افقی را تنها میخواهید به اعضای فضای نمونه محدود کنید که با روش مشابه آمده در پاسخی که برای پرسش پیشینتان فرستادم میبینید. یا اینکه میتوانید به شکل نمودار یک تابع با دامنهٔ کل $\mathbb{R}$ بکشید مانند زیر (که دستور Mathematicaیِ آن را نیز گذاشتهام).
P1=Plot[Piecewise[{{0,x<1},{0.6,1<=x<5},{0.9,5<=x<10},{1,x>=10}}],{x,-1,12},ExclusionsStyle->{{Red,Dashed},None},PlotStyle->Directive[Thickness[0.01],Blue]];
emptyPoints={{1,0},{5,0.6},{10,0.9}};
P2=ListPlot[emptyPoints,PlotMarkers->"OpenMarkers"];
filledPoints={{1,0.6},{5,0.9},{10,1}};
P3=ListPlot[filledPoints,PlotMarkers->{Automatic,Small}];
Show[P1,P2,P3,AxesLabel->{ToExpression["x",TeXForm,HoldForm],ToExpression["F_X(x)",TeXForm,HoldForm]},LabelStyle->Directive[Black,16],Ticks->{{1,5,10},{0,0.6,0.9,1}}]
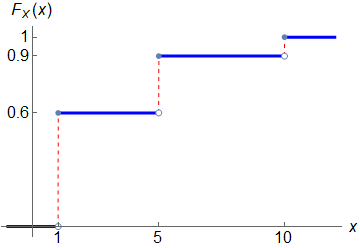
پیوند به پاسخی که برای پرسش دیگرتان فرستادهبودم: https://math.irancircle.com/20081/#a20119