همانگونه که خودتان اشاره کردید، اگر قرار دهیم $f(x)=\sqrt{x^3-x^2}$ (و فقط ریشهٔدومِ مثبت را از رادیکال بپذیریم) آنگاه این ضابطه، بر روی دامنهاش یعنی $[1,+\infty)$ تابعی یکبهیک است. برای وارونش همانگونه که دوباره خودتان گفتید نقش $x$ و $y$ را جابجا و اقدام به حلِ برابریِ $y^3-x^2-x^2=0$ بر حسب $y$ میکنیم. چون چندجملهایِ درجه ۳ است میتوان از فرمول استفاده کرد. چون فرمول قدری ناکوتاه است به این صفحهٔ ویکیپدیا ارجاع میدهیم که میتوانید این فرمول را ببینید (اینجا کلیک کنید). من به جای انجام دستیِ این کار از نرمافزار Maple کمک گرفتم.
solve(y^3-y^2-x^2=0,y);
که از سه خروجیِ این دستور تنها یکی یک تابع بر حسب $x$ و بدون عدد موهومی مختلط است و ما هم همان را نیاز داریم. این ضابطه به شکل زیر است:
$$\frac{\left(8+108 x^{2}+12 \sqrt{81 x^{4}+12 x^{2}}\right)^{\frac{1}{3}}}{6}+\frac{2}{3 \left(8+108 x^{2}+12 \sqrt{81 x^{4}+12 x^{2}}\right)^{\frac{1}{3}}}+\frac{1}{3}$$
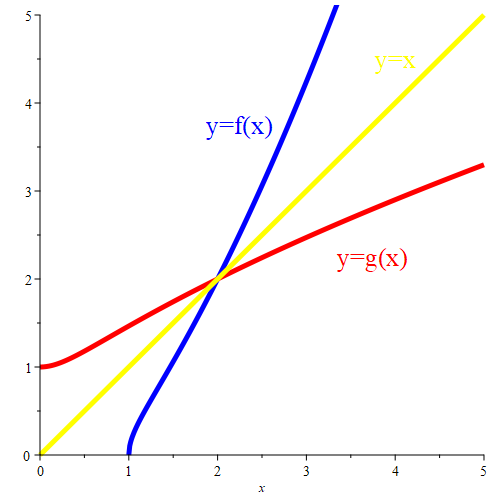
آن را $g(x)$ بنامید. در زیر نمودار تابعهای $f$ و $g$ به همراه نیمساز یکچهارم یکُم آوردهشدهاست.