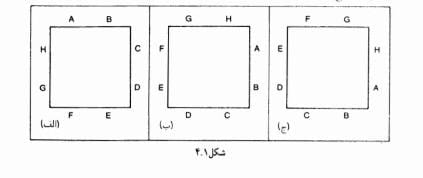
ШЁЩҮ ЪҶЩҶШҜ ШұШ§ЩҮ Щ…ЫҢШӘЩҲШ§ЩҶ 8 ЩҶЩҒШұ ШұШ§ Ъ©ЩҮ ШЁШ§ A, B, C, ...., H ЩҶШҙШ§ЩҶ ШҜШ§ШҜЩҮвҖҢШ§ЫҢЩ… ШЁЩҮ ШҜЩҲШұ Щ…ЫҢШІ Щ…ШұШЁШ№ ШҙЪ©Щ„ ШЁЩҶШҙШ§ЩҶЫҢЩ…ШҢ Ъ©ЩҮ ШҜШұ ШўЩҶ ШҙЪ©Щ„вҖҢЩҮШ§ЫҢ 4.1(Ш§Щ„ЩҒ) ЩҲ 4.1(ШЁ) ЫҢЪ©ЫҢ ШЁЩҮ ШӯШіШ§ШЁ Щ…ЫҢвҖҢШ§ЫҢЩҶШҜ Ш§Щ…Ш§ Ш§ШІ ШҙЪ©Щ„ 1.4(Ш¬) Щ…ШӘЩ…Ш§ЫҢШІЩҶШҜШҹ
Щ…ЫҢШҜЩҲЩҶЩ… Ъ©ЩҮ Ш¬Ш§ЫҢЪҜШҙШӘ ШҜЩҲШұЫҢ ШЁШұШ§ЫҢ Щ…ЫҢШІ ЪҜШұШҜ (n-1)! Щ…ЫҢШЁШ§ШҙШҜ Ш§Щ…Ш§ Ъ©ШіЫҢ Ш§ЫҢШҜЩҮвҖҢШ§ЫҢ ШЁШұШ§ЫҢ Ш§ЫҢЩҶ Щ…ШіШҰЩ„ЩҮ ШҜШ§ШұЩҮШҹ ЩҫШ§ЫҢЫҢЩҶШӘШұ Щ…ЩҶШ·ЩӮ Ш§ШөЩ„ЫҢ ШЁШҜШіШӘ Ш§ЩҲШұШҜЩҶ ЩҒШұЩ…ЩҲЩ„ (n-1)! ШұЩҲ ЩҶЩҲШҙШӘЩ… ЪҜЩҒШӘЩ… ШҙШ§ЫҢШҜ ШЁШ§ЫҢШҜ Ш§ШІ Ш§ЩҲЩҶ ШЁШҜШіШӘ ШЁЫҢШ§ШҜ ЩҲЩ„ЫҢ Щ…Ш·Щ…Ш№ЩҶ ЩҶЫҢШіШӘЩ….
.
.
.
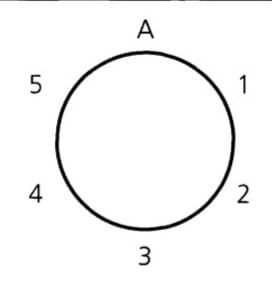
Ш§ЪҜШұ ШЁШ®ЩҲШ§ЩҮЫҢЩ… 6 ЩҶЩҒШұ Ъ©ЩҮ ШЁШ§ A, B, ... , F ЩҶШҙШ§ЩҶ Щ…ЫҢШҜЩҮЫҢЩ… ШҜЩҲШұ Щ…ЫҢШІ ЪҜШұШҜЫҢ ШЁЩҶШҙШ§ЩҶЫҢЩ…ШҢ Ш¬Ш§ЫҢ ЩҶЩҒШұ Ш§ЩҲЩ„ (A) ШұШ§ Щ…ШҙШ®Шө Щ…ЫҢЪ©ЩҶЫҢЩ…. Ш§ЫҢЩҶЪ©ЩҮ A Ъ©Ш¬Ш§ ШЁЩҶШҙЩҶШҜ ЩҮЫҢЪҶ ШӘЩҒШ§ЩҲШӘЫҢ Ш§ЫҢШ¬Ш§ШҜ ЩҶЩ…ЫҢЪ©ЩҶШҜ. ЩҲ ШіЩҫШі ЩҶЩҲШ№ ЩҶШҙШ§ЩҶШҜЩҶ 5 ЩҶЩҒШұ ШЁШ№ШҜЫҢ ЫҢЪ© Ш¬Ш§ЫҢЪҜШҙШӘ Ш®Ш·ЫҢ Ш®ЩҲШ§ЩҮШҜ ШЁЩҲШҜ.