مشتق پذیری توابع قدر مطلق و نوشتن دامنه و برد آنها

Question

سلام خسته نباشید مشتق و دامنه و برد مشتق و رسم نمودار تابع | y= | x رو میتونید با فرمولی که در کتاب ریاضی دوازدهم تجربی اومده حل کنید؟

Answer 1

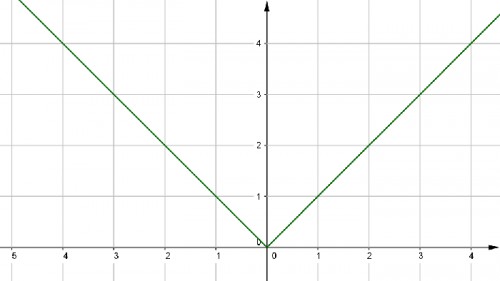
نمودار تابع $y=|x|$ به شکل زیر است

باتوجه تعریف مشتق

$f'(a)= \lim_{x\to a} \frac{|x|-|a|}{x-a}=\lim_{x\to a} \frac{(|x|-|a|)(|x|+|a|)}{(x-a)(|x|+|a|)}=\lim_{x\to a} \frac{x^2-a^2}{(x-a)(|x|+|a|)}=\lim_{x\to a} \frac{x+a}{|x|+|a|} $

زمانی این حد موجود و لذا مشتق وجود خواهد داشت که $ a \neq 0 $و

$ f'(a)= \lim_{x\to a}\frac{a}{|a|}=\begin{cases}1 & a>0\\-1 & a<0\end{cases} $

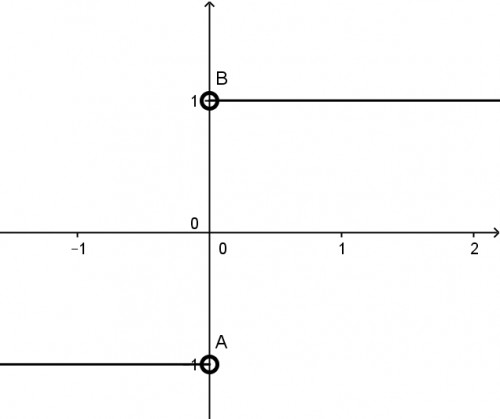
به این ترتیب دامنه تابع مشتق $R- \{0\} $ و برد آن $ \{ \mp 1\} $ است.ونمودار تابع مشتق به صورت زیر خواهد بود.

Comments

$y=|u| \Rightarrow y'= \frac{u'u}{|u|}$

کهu تابعی از x باشد