Question

با استفاده از قضیه رول نشان دهید که معادله tanx=1-x در فاصله (1و0) جواب دارد. راهنمایی: از تابع f(x)=(1-x)sinx کمک بگیرید.

Comments

@Khose_M2 خودتان چه فکری کردید؟ اصلا صورت قضیهٔ رول را خوانده‌اید؟

---

@AmirHosein به دل ما موند شما جواب یه سوال رو مرحمت کنین و بنویسین.

Answer 1

همان طور که خود شما گفتید تابع $f(x)= (1-x)\sin(x)$ را در نظر بگیرید.این تابع روی بازه $[0,1]$ پیوسته و روی بازه $(0,1)$ مشتقپذیر است. چون $f(0)=f(1)=0$ دست کم یک نقطه به طول $x_0$ هست که $f'(x_0)=0$ یعنی:

$$-\sin(x_0)+(1-x_0)\cos(x_0)=0$$

اگر طرفین را بر $\cos(x_0)$ تقسیم کنیم خواهیم داشت :

$$\color{green}{\tan(x_0)=1-x_0}$$

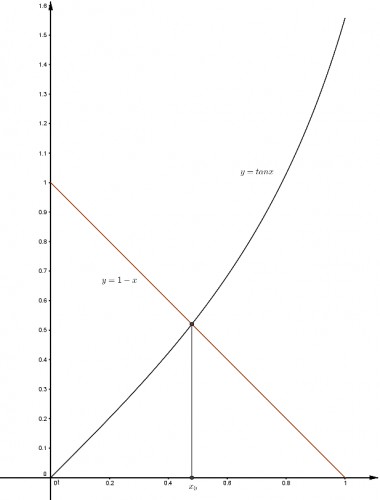
واین معنایش این است که این معادله جوابی در این فاصله خواهد داشت.

Comments

@good4us خود پرسش‌کننده راهنمایی را نگفته‌است، احتمالا در کتاب یا هر جایی که این پرسش را دیده‌اند، جلویش نوشته بوده‌است «راهنمایی: ...» و ایشان هم به عنوان قسمتی از پرسش کپی کرده‌اند اینجا.

---

@good4us ممنون. درست حدس زدید. راهنمایی هم قسمتی از صورت سوال بود. من متوجه نشدم به چه شکلی
cos(1-x)=sinx
رو به دست اوردین

---

Khode_M2@
من این را cos(1-x)=sinx که نوشته اید ننوشته ام به دقّت به دیدگاه خودتان و پاسخ من نگاه کنید.