به نام خدا.
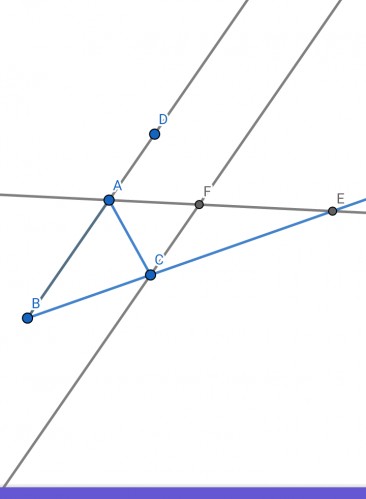
در شکل بالا نیمساز خارجی زاویه A در مثلث $ABC$ ضلع $BC$ را در $E$ قطع کرده است. حال از $C$ خطی موازی با AB رسم می کنیم تا نیمساز را در $F$ قطع کند. داریم:
$CF \parallel AB \Longrightarrow \angle CAF= \angle CFA \Longrightarrow CF=AC$
حال با توجه به قضیه تالس:
$ \frac{BE}{CE} = \frac{AB}{CF} = \frac{AB}{AC} $