تعداد دانش اموزانی را مشخص کنید که به هر سه رشته ورزشی علاقه دارند

Question

در یک کلاس ۳۲ نفره ۳ نفر از دانش اموزان به هیچ یک از رشته های فوتبال والیبال و بسکتبال علاقه ندارند ۱۶ نفر به فوتبال ۱۴ نفر به والیبال ۱۴ نفر به بسکتبال ۶ نفر به فوتبال و والیبال ۵ نفر به والیبال و بسکتبال و ۶ نفر به فوتبال و بسکتبال علاقه‌مند هستند تعداد دانش اموزانی را مشخص کنید که :

الف)به هر سه رشته ورزشی علاقه دارند ب)فقط به فوتبال علاقه دارند پ)فقط به بسکتبال علاقه دارند ت)فقط به والیبال علاقه دارند ث)به فوتبال علاقه دارند ولی به والیبال علاقه ندارند ح)به والیبال علاقه دارند ولی به بسکتبال علاقه ندارند

Comments

@hosseinscooter اصلا پیش از ارسال پرسش به پرسش‌های مشابه در سایت نگاه کرده‌اید؟ ابتدا باید خودتان تلاش کنید و در سایت نیز جستجو کنید و اگر پرسش مشابهی هست از پاسخ آن ایده بگیرید. اگر هنوز نتوانستید حل کنید، آنگاه به عنوان پرسش جدید ارسال کنید و بعلاوه به تلاش خود در متن پست‌تان اشاره کنید نه اینکه فقط متن سوال را بنویسید. برای نمونه یک پرسش خیلی مشابه
https://math.irancircle.com/8489

---

بله  - بنده اتفاقا از طریق سرچ و دیدن همین سوالی که لینکشو فرستادید با این سایت آشنا شدم - دنبال گرفتن ایده نیز بودم - چرا ایده نگرفتم ؟ چون پاسخی پیدا نکردم !!! نوشته پاسخ در فایل پیوست ولی فایل پیوستی ندیدم میشه راهنمایی کنید از کجا باید فایل پیوست رو پیدا کنم - واینکه من بگم تلاش کردم و نکردم واقعا در صورت مسئله فرقی میکنه ؟ بخدا کلی فکر کردم و تقریبا 70 درصد مسئله رو حل کردم فقط تعداد فوتبالیها درست درنمیومد - بعد چه جوری این همه راه حل رو بنویسم ، نمیشه تصویر آپلود کرد

Answer 1

فرض کنید $S$ مجموعه افراد کلاس است پس $ \mid S \mid =32$ . فرض کنید $A$ مجموعه افراد علاقه مند به فوتبال ، $B$ مجموعه افراد علاقه مند به والیبال و $C$ مجموعه افراد علاقه مند به بسکتبال است . پس :

$$ \mid A \mid =16 \ \ \ \ \mid B \mid = 14 \ \ \ \ \ \mid C \mid =14 $$

طبق فرض $3$ نفر در کلاس به هیچ رشته ای علاقه ندارند پس $32-3=29$ نفر علاقه مند به حداقل یکی از رشته های مذکور هستند . پس :

$$ \mid A \cup B \cup C \mid =29$$

همچنین طبق فرض $6$ نفر به فوتبال و والیبال علاقه مند هستند پس $ \mid A \cap B \mid =6$ و $5$ نفر به والیبال و بسکتبال علاقه مند هستند پس $ \mid B \cap C \mid =5$ و $6$ نفر به فوتبال و بسکتبال علاقه مند هستند پس $ \mid A \cap C \mid =6$ .

حال طبق فرمول اصل شمول و عدم شمول داریم :

$$ \mid A \cup B \cup C \mid =\mid A \mid+\mid B \mid+\mid C \mid-\mid A \cap B \mid-\mid A \cap C \mid-\mid B \cap C \mid+\mid A \cap B \cap C \mid$$

با جاگذاری خواهیم داشت :

$$29=16+14+14-6-6-5+\mid A \cap B \cap C \mid$$

پس :

$$\mid A \cap B \cap C \mid=2$$

یعنی $2$ نفر به هر $3$ رشته علاقه مند هستند .

با توجه به اطلاعات بالا می توان نمودار ون زیر را رسم کرد . مستطیل بیانگر کلاس ، دایره ها بیانگر مجموعه های $A,B,C$ و اعداد داخل هر ناحیه بیانگر تعداد دانش آموزانی هستند که در آن ناحیه قرار می گیرند :

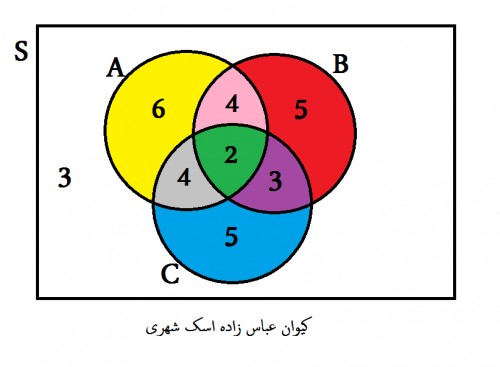
توجه کنیم در بالا بدست آوردیم که $2$ نفر به هر $3$ رشته ورزشی علاقه دارند پس در ناحیه سبز رنگ که ناحیه اشتراک $3$ مجموعه است $2$ نفر قرار می گیرند . از طرفی طبق فرض $6$ نفر به فوتبال و والیبال علاقه دارند پس در ناحیه های سبز و صورتی که نواحی مشخص کننده اشتراک دو مجموعه $A$ و $B$ هستند جمعا $6$ نفر قرار می گیرند . بنابراین در ناحیه صورتی باید $6-2=4$ نفر قرار گیرند . به همین ترتیب در مورد نواحی دیگر عمل می کنیم .

حال می توانیم به قسمت های دیگر سوال جواب دهیم :

ب) فقط به فوتبال علاقه دارند : این افراد در نمودار ون در ناحیه زرد رنگ قرار می گیرند که تعداشان $6$ نفر است .

پ) فقط به بسکتبال علاقه دارند : این افراد در ناحیه آبی رنگ قرار می گیرند که تعداشان $5$ نفر است .

ت) فقط به والیبال علاقه دارند : این افراد در ناحیه قرمز رنگ قرار می گیرند که تعداشان $5$ نفر است .

ث) به فوتبال علاقه دارند ولی به والیبال نه : این افراد در نواحی زرد و خاکستری قرار می گیرند که تعداشان $6+4=10$ نفر است .

ح) به والیبال علاقه دارند ولی بسکتبال نه : این افراد در نواحی صورتی و قرمز قرار می گیرند که تعداشان $4+5=9$ نفر است .

Comments

کجا میتونم امیتاز بدم ؟
قسمت امتیاز دهی خاموش است
اگر با کامنت قبول است 20 امتیاز برای ایشان

---

@hosseinscooter
شما هنوز به اندازه کافی امتیاز ندارید که بتوانید به کاربران دیگر امتیاز دهید.
فعلا فقط می توانید پاسخی را به عنوان بهترین پاسخ انتخاب کنید.

Answer 2

سلام

تعداد کل دانش آموزان 34 نفر است اما 3 نفر از آن ها به هیچ ورزشی علاقه ندارند؛در نتیجه سوال رو با توجه به تعداد دانش آموزان علاقه مند به ورزش پیش می بریم(29=3-32):

فوتبال = F

بسکتبال = B

والیبال = V

تعداد کل علاقه مندان به ورزش = M = $n(F \cup B \cup V)$ $$$$</math> بر اساس فرمول زیر: <math>$$ n(A \cup B \cup C)=n(A)+n(B)+n(C)-n(A \cap B)-n(A \cap C)-n(B \cap C)+n(A \cap B \cap C)$$</math> نتیجه می گیریم: <math>$$29 = n(F) + n(B)+n(V)-n(F \cap B)-n(F\cap V)-n(B\cap V)+n(F\cap B \cap V)=$$</math> <math>$$29= 16 + 14 + 14-6-5-6+n(F\cap B\cap V)$$</math> <math>$$ \rightarrow n(F\cap B\cap V)=2$$</math> <math>$$$$

پس جواب قسمت الف بدست آمد حالا می توانید با استفاده از نمودار ون بقیه سوال ها رو جواب بدید(البته به شکل جبر مجموعه ها هم میشه ادامه داد اما این روش راحت تر و مفهومی تره)

Comments

بسیار عالی