Question

در مثلث AB=6 ABC، و AC=7 و عمود منصف های این دو ضلع بر هم عمود میباشند فاصله نقطه تلاقی عمود منصف ها از وسط بزرگترین ضلع مثلث چقدر است؟ گزینه ۱:یک دوم گزینه ۲:یک چهارم گزینه۳:صفر گزینه ۴:رادیکال دو دوم

Answer 1

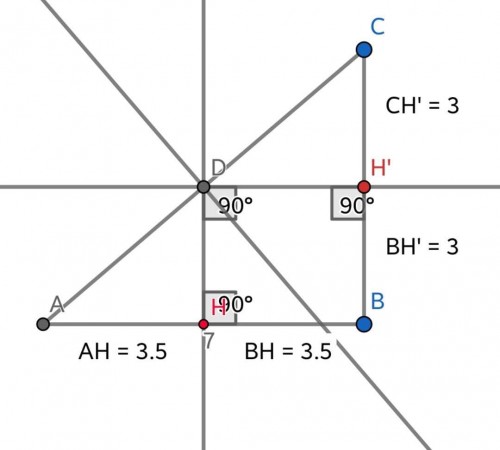
همان گونه که در شکل بالا مشاهده می کنید، اندازه زاویه های $D,H,H'$ برابر با 90 درجه است. چون $B+H+D+H'=360$ پس اندازه زاویه $B$ نیز برابر 90 درجه است. در نتیجه چهارضلعی $BHDH'$ مستطیل است ، پس $DH'=3.5,DH=3$ و $DH | BH'$ و $DH' | BH$ است و چون $ \frac{DH'}{AB}= \frac{CH'}{BC} $ پس راس $D$ روی ضلع $AC$ قرار دارد. باتوجه به اینکه راس $D$ همرسی عمود منصف هاست و چون روی ضلع $AC$ قرار دارد پس راس $D$ روی مرکز پاره خط $AC$ قرار دارد پس فاصله راس $D$ از مرکز $AC$، برابر صفر است.