توجه کنید که دو متغیر تصادفی پیوسته دارید، بدون کاستن از کلیت ساعت ۱۰ را مبدأ زمانی بگیرید، در این صورت میتوانید متغیر تصادفیِ زمانِ رسیدن نفر نخست را $X$، یک متغیر تصادفی یکنواخت پیوسته بگیرید که از بازهٔ بستهٔ ۰ تا ۶۰ دقیقه پس از مبدأ زمانیمان گزینش میشود. به همین صورت رسیدن بین ساعت ۱۰:۲۰ و ۱۱:۲۰ یعنی بازهٔ بستهٔ ۲۰ تا ۸۰ (۸۰ دقیقه پس از ساعت ۱۰ میشود ساعت ۱۱:۲۰). پس متغیر تصادفی دوم را $Y$ بنامید که یک متغیر تصادفی یکنواخت از بازهٔ $[20,80]$ است. اینک پیشآمد خواستهشده این است که $Y<X$ (نفر دوم زودتر از نفر نخست رسیدهباشد). پس شکل زیر را دارید.
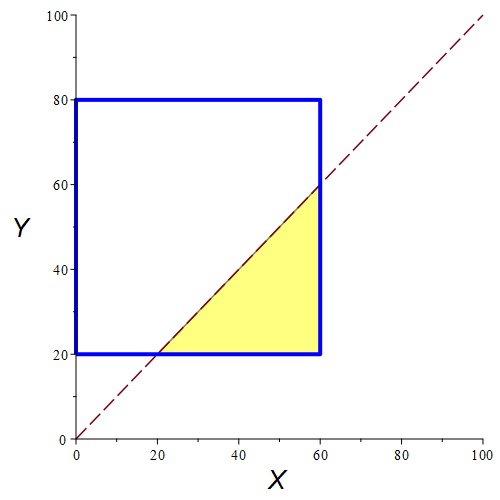
کل فضای نمونه مربع آبیرنگ و داخلش است، و فضای پیشامد اشتراک فضای نمونه با بخش زیر خطِ رسمشده که خطِ $y=x$ است میباشد. این ناحیه سهگوش رنگشده به رنگِ زیرد است. احتمالِ روی دادنِ این پیشامد برابر است با مساحت ناحیهٔ زردرنگ تقسیم بر مساحت مربع با مرزِ آبیرنگ. توجه کنید که گوشهٔ سمت چپ این سهگوش دارای پهنا (عرض) -ِ ۲۰ است و درازا (طول) آن از برابریِ $y=x$ (چون رو خط است) همان ۲۰ بدست میآید. به روش یکسان مختصات گوشهٔ بالاییِ سهگوش $(60,60)$ است.
$$\frac{\frac{(60-20)(60-20)}{2}}{(60-20)(80-20)}=\frac{\frac{40\times 40}{2}}{60\times 60}=\frac{2}{9}$$
اگر علاقه به استفاده از انتگرالها دارید آنگاه احتمالِ خواستهشده به شکل زیر نوشته میشود که برای یک مجموعهٔ دلخواه، $\chi_A$ به معنای تابع عضوبودن در $A$ است. یعنی برای هر مقدارِ $(x,y)\in\mathbb{R}^2$ مقدارِ $\chi_{Y<X}(x,y)$ برابر با ۱ است اگر و تنها اگر $(x,y)\in\lbrace (x,y)\in\mathbb{R}^2\mid y<x\rbrace$ و در غیر اینصورت برابر با صفر است.
$$\frac{\int_0^{60}\int_{20}^{60}\chi_{Y<X}(x,y)dydx}{\int_0^{60}\int_{20}^{60}dydx}$$
این انتگرال را میتوانید دستی حل کنید و به پاسخ بالا برسید. ولی اینجا با کمک نرمافزار Maple این انتگرالها را حل میکنیم. نخست برای انتگرال صورت کسر:
int( int( piecewise( y < x, 1, 0), y = 20 .. 80 ), x = 0 .. 60 );
که Maple پاسخِ ۸۰۰ را به ما برمیگرداند. برای انتگرال مخرج:
int( int( 1, y = 20 .. 80 ), x = 0 .. 60 );
که به ما ۳۶۰۰ را برمیگرداند. اکنون ۸۰۰ تقسیم بر ۳۶۰۰ که به $\frac{2}{9}$ ساده میشود پاسخ ما است.