سلام
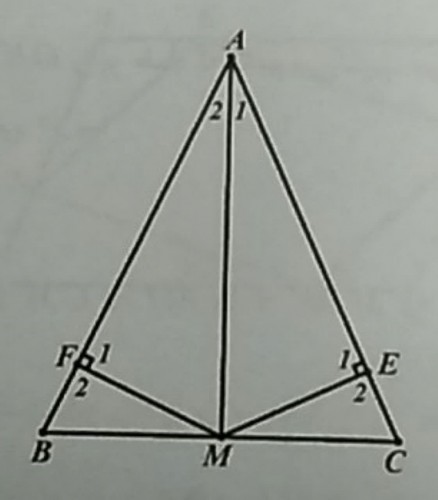
ابتدا آن مثلث را $ABC$ در نظر میگیریم.سپس میانه $AM$ را در این مثلث رسم میکنیم و پای عمود های وارد از $M$ بر اضلاع $AC$ و $AB$ را به ترتیب $E$ و $F$ می نامیم. حال داریم:
$ E_{1}= F_{1}=90 , AM=AM , A_{1}= A_{2} \} \Longrightarrow \bigtriangleup AME= \bigtriangleup AMF \Rightarrow AE=AF , ME=MF $
$ E_{2}= F_{2}=90 , MC=MB , ME=MF \} \Longrightarrow \bigtriangleup MCE= \bigtriangleup MBF \Rightarrow CE=BF(2) $
با جمع روابط یک و دو نتیجه میگیریم :
$AE+CE=AF+BF \Rightarrow AC=AB$
شکل :