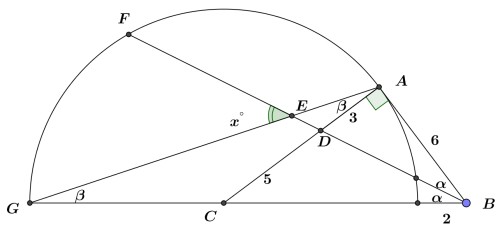
باتوجه به اینکه $BA$ بر دایره مماس است مثلث $BAC$ قائم الزاویه است . گیریم $AD=y$
$$ (5+y)^{2}+36=(7+y)^{2} \Rightarrow y=3 $$
چون خواهیم داشت: $ \frac{AB}{AD}=\frac{CB}{CD}=2 $ پس $ BF$ نیمساز زاویه $ ABG$ است.
درمثلث $ ABG$ خواهیم داشت: $2 \alpha +2 \beta = 90^{ \circ } \Rightarrow \alpha + \beta = 45^{ \circ } $
از طرفی زاویه $FEG$ زاویه خارجی مثلث $ EBG$ و برابر$\color{RED}{ \alpha + \beta = 45^{ \circ }} $ است (لذا $x=45$)