ميخواهيم مساحت قطاع دايره را پيدا كنيم.كه ابتدا قطاع دايره را تعريف ميكنيم
قطاع دايره:قسمتي از از دايره است كه بين دوشعاع دايره محصور شده است
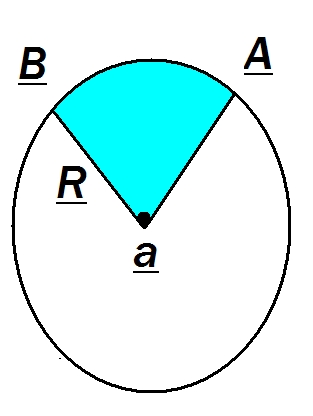
ما ميدانيم مساحت دايره برابراست با$({ \pi} R^{2}) $ ومساحت نيم دايره برابر با$ \frac{({ \pi} R^{2})}{2} $
بنابراين ميتوانيم بگوييم مساحت قطاع دايره با زاويه $( \ 180)$يا$({ \pi}) rad$
برابر است با$ \frac{({ \pi} R^{2})}{2} $
حال براي مساحت قطاع دايره با هر زاويه ايي مانند$( \alpha )$به يك تناسب ساده نياز داريم يعني
برحسب درجه:$$(180) \longrightarrow \frac{({ \pi} R^{2})}{2} $$
$$ \alpha \longrightarrow S_{ \alpha } $$
برحسب $rad$:$$({ \pi}) \longrightarrow \frac{({ \pi} R^{2})}{2} $$
$$ \alpha \longrightarrow S_{ \alpha } $$
بنابراين
مساحت قطاع دايره با شعاع$R$و زاويه$ \alpha $,برابرست با:$$S= \frac{R^{2} \alpha }{2} = \frac{ \alpha { \pi} R^{2} }{360} $$
حال مساحت قطعه دايره را پيدا ميكنيم ابتدا آنرا تعريف ميكنيم
قطعه دايره:قسمتي از دايره است كه بين وتر و كمان مربوط به وتر محصور شده است(اگر منظوراز قطعه اين باشد)
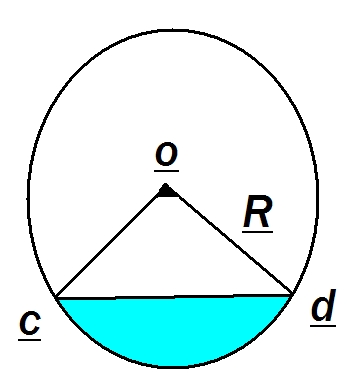
حال اگرمساحت قطاع دايره را با$ S_{1} $و مساحت مثلث را با $ S_{2} $نشان دهيم
داريم$$S= S_{1} - S_{2} \Rightarrow S= \frac{ R^{2} \alpha }{2} - \frac{OC.OD.sin \alpha }{2} $$
$$ \Rightarrow S= \frac{ R^{2} \alpha }{2} - \frac{R.R.sin \alpha }{2} $$
$$ \Rightarrow S= \frac{ R^{2} ( \alpha -sin \alpha )}{2} $$
بنابراين
مساحت قطعه دايره با شعاع$R$و زاويه ي$ \alpha $برابر است با:$$ \ S= \frac{ R^{2} ( \alpha -sin \alpha )}{2} $$