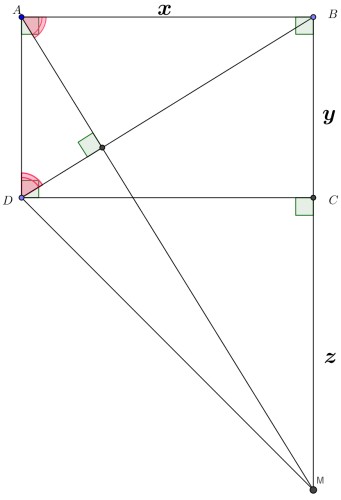
چون مثلث های $BAD$ و $ABM$ به حالت دو زاویه مساوی متشابهند:
$ \frac{x}{y}= \frac{y+z}{x} $
از طرفی چون داریم : $ \frac{x}{y}= \frac{y+x}{x} $و باتوجه به برقراری رابطه طلایی پس $z=x$ و لذا در مثلث قائم الزاویه متساوی الساقین $DCM$ خواهیم داشت
$DM= \sqrt{2}x \Rightarrow \color{red}{x= \frac{\sqrt{2}}{2}DM} $