Щ„Щ…
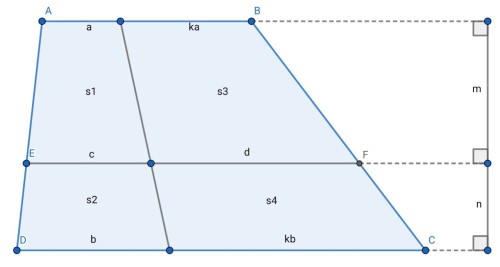
ЩҫШ§ШұЩҮ Ш®Ш·
$EF$
Щ…ЩҲШ§ШІЫҢ ЩӮШ§Ш№ШҜЩҮ ЩҮШ§ЫҢ Ш°ЩҲШІЩҶЩӮЩҮ
$ABCD$
Ш§ШіШӘ.
ШҜШ§ШұЫҢЩ…:
$d=kc$
Ш§Ш«ШЁШ§ШӘ
$\frac{2(s3+s4)}{2(s1+s2)}=\frac{(ak+bk)(m+n)}{(a+b)(m+n)}=k$
$\Rightarrow 2(s3+s4)=2k(s1+s2)$
$\Rightarrow(ka+d)m+(kb+d)n=k(a+c)m+k(b+c)n$
$\Rightarrow kam+dm+kbn+dn=kam+kcm+kbn+kcn$
$\Rightarrow dm+dn=kcm+kcn$
$\Rightarrow d(m+n)=kc(m+n)$
ЩҲ ШҜШұ ЩҶЩҮШ§ЫҢШӘ ШҜШ§ШұЫҢЩ…:
$\Rightarrow d=kc$
Щ…ШіШҰЩ„ЩҮ
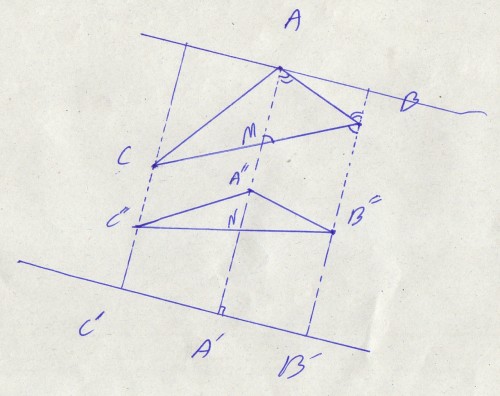
ШҜШұ Ш°ЩҲШІЩҶЩӮЩҮ
$BCC'B'$
ШҜШ§ШұЫҢЩ…:
$CC''=C'C''$
$BB''=B'B''$
ЩҲ ЩҮЩ…ЪҶЩҶЫҢЩҶ
$A'M$
Щ…ЩҲШ§ШІЫҢ ШҜЩҲ ЩӮШ§Ш№ШҜЩҮ Ш§ШіШӘ ЩҫШі ШЁШ§ ШӘЩҲШ¬ЩҮ ШЁЩҮ Щ„Щ… Ш®ЩҲШ§ЩҮЫҢЩ… ШҜШ§ШҙШӘ:
$A'N=MN\Rightarrow A'N=\frac{A'M}{2}\qquad(k=1)$
ЩҲ ШЁШ§ ШӘЩҲШ¬ЩҮ ШЁЩҮ ЩҒШұШ¶ Щ…ЫҢШҜШ§ЩҶЫҢЩ…:
$A'A''=\frac{AA'}{2}$
ШЁЩҶШ§ШЁШұ ШӘШіШ§ЩҲЫҢ ЩҮШ§ЫҢ ШЁШ§Щ„Ш§ ЩҶШӘЫҢШ¬ЩҮ Щ…ЫҢЪҜЫҢШұЫҢЩ…:
$A''N=A'A''-A'N=\frac{AA'}{2}-\frac{A'M}{2}=\frac{AA'-A'M}{2}=\frac{AM}{2}\Rightarrow \frac{AM}{A''N}=2$
ЩҲ ШҜШұ ЩҶЩҮШ§ЫҢШӘ:
$\frac{S_{ABC}}{S_{A''B''C''}}=\frac{S_{ABM}+S_{ACM}}{S_{A''B''N}+S_{A''C''N}}=\frac{\frac{1}{2}(AM\cdot A'B'+AM\cdot A'C')}{\frac{1}{2}(A''N\cdot A'B'+A''N\cdot A'C')}=\frac{AM\cdot(A'B'+A'C')}{A''N\cdot(A'B'+A'C')}=\frac{AM}{A''N}=2$