چرا Ox نیم ساز است؟

Question

سوزن پرگار را بر راس زاویه می گذاریم ودو کمان با شعاع مختلف می زنیم.بر زاویه 4 نقطه به دست می آید.به کمک این 4نقطه دو خط متقاطع رسم می کنیم. نقطه تقاطع را به راس زاویه وصل می کنیم.چرا این خط نیم ساز زاویه است؟

Answer 1

بنابر فرض $OA=OB$ و $OD=OC$ و زاویه $O$ بین دو مثلث $OAD$ و $OBC$ مشترک است لذا این دو مثلث بنابر حالت دوضلع و زاویه بین با هم همنهشت می باشند.

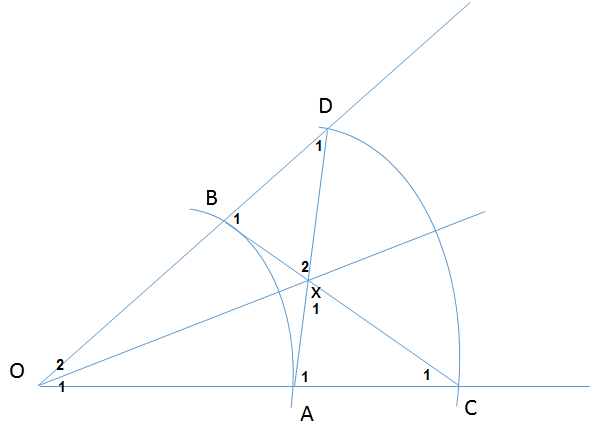
بنابراین $\hat D_1=\hat C_1$ و چون $\hat x_1$و $\hat x_2$ متقابل به راس اند لذا $\hat x_1=\hat x_2$ بنابر این بنابر مجموع زوایای داخلی مثلث باید $A_1=B_1$ . ولی چون $BD=AC$ لذا بنابر حالت دو زاویه و ضلع بین مثلث های $xAC$ و $xBD$ هم نهشت هستند بنابراین $Ax=Bx$ ولی از طرفی $OA=OB$ و $Ox$ هم مشترک است لذا مثلث های $OAx$ و $OBx$ بنابر حالت سه ضلع هم نهشت هستند به همین دلیل $\hat O_1=\hat O_2$ . یعنی $Ox$ نیم ساز است.

Comments

OAC مثلث نیست

---

@bf124
درسته منظورم $xAC $بود.
ویرایش کردم. ممنون