روش پولیا
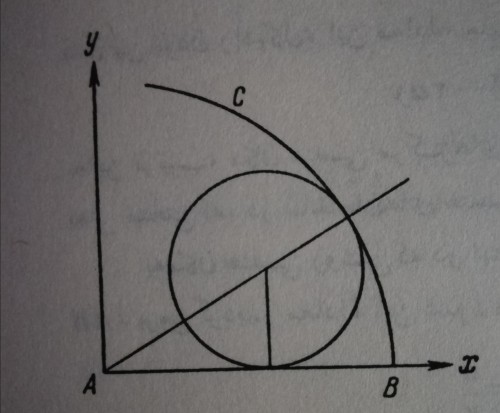
فعلا کمان AC در نظر نمی گیرم. ابتدا مکان هندسی مراکز دایره هایی که بر پاره خط AB به طول A و کمان AC. مماس هستند پیدا می کنیم. مختصات مرکز دایره مماسی را
$O=(x, y)
$
نظر می گیریم در نتیجه شعاع آن r=y می باشه، بنابراین
$$R=AO+r \Rightarrow y=a-\sqrt{x^2 +y^2}
$$
که مکان هندسی معادله سهمی زیر می باشه.
$$x^2 =a^2 - 2ay
$$
حال می توان برای جواب سوال، کمان AC رسم کرد در این صورت خواهیم داشت
$$x= \frac{a}{2} \Rightarrow y= \frac{3a}{8}
$$