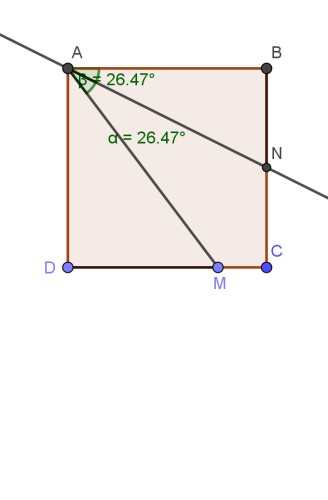
اگر طول هرضلع مربع را $a$ بگیریم با توجه به شکل اندازه زاویه $AMD$ برابر $2 \alpha $ و $ \alpha = \beta $
$ tan \alpha= \frac{BN}{a} و tan 2 \alpha = \frac{2tan \alpha}{1-tan^2 \alpha} = \frac{a}{DM} $
با جایگزینی مقدار $tan \alpha$
$ \frac{2BN}{a^2-BN^2} = \frac{1}{DM} \Rightarrow a^2+DM^2=(BN+DM)^2= AM^2=(BN+DM)^2 $
$ \Rightarrow \color{red}{ AM= BN+DM}$