از تساوی بالا به کمک نمودار ون می توان نتیجه گرفت کهA فقط با B یا فقط با C اشتراک ندارد یعنی اگر A با B اشتراک داشته باشه آنگاه با C هم اشتراک داره بنابراین شمارش حالتها با اشتراک سه مجموعه می شماریم. اشتراک سه مجموعه D در نظر می گیریم. یعنی
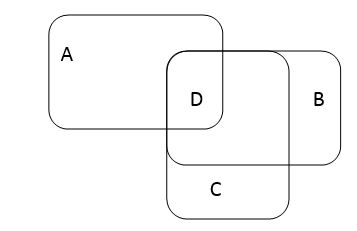
5 حالت زیر با کمک نکته زیر برای Dداریم:
نکته مهم: تعداد انتخاب مجموعه های X وY که در رابطه زیر صدق می کنند برابر
$3^n
$
$$X \bigcup Y= \{1,2,3,...,n\}
$$
حالت اول) D مجموعه 4 عضوی باشه در این صورت فقط یک حالت داریم یعنی
D=A=B=C
حالت دوم( D سه عضوی باشه در این صورت انتخاب D چهار طریق می باشه اما انتخاب سه مجموعه روی عضو چهارمی به یکی از دو زیر است
اگر مجموعه A همان D باشه مچموعه هایB وC به سه طریق عضو چهارم دارند و اگرA عضو چهارم داشته باشه آنگاه B وC عضو چهارم ندارند. بنابراین در این حالت به 16 طریق انجام می شود. (4 در 4)
حالت سوم( D یه مجموعه 2 عضوی باشه پس D به 6 طریق میتوان انتخاب کرد اگرAهمان دو عضو اشتراک باشه آنگاه B اجتماع Cبه 9 طریق می توان انتخاب کرد (نکته مهم) پس در این حالت هم 54 طریق می توان شمرد. و اگر A یه عضو سومی داشته باشه(2) آنگاه B اجتماع Cبه 3 طریق می توان انتخاب کرد (نکته مهم) پس در این حالت هم 6 طریق می توان شمرد و اگرA همان مجموعه چهار عضوی باشه بنابه حالت اول یک حالت داریم در نتیجه حالت سوم 61 می باشه
حالت چهارمD یک عضوی باشه پس D به 4 طریق بدست می آید اگرA همان یک عضو یعنیD باشه آنگاه B اجتماع Cبه 27 طریق می توان انتخاب کرد (نکته مهم) پس در این حالت هم 108 طریق می توان شمرد. اگر A یه عضو دومی داشته باشه(3) آنگاه B اجتماع Cبه 9 طریق می توان انتخاب کرد (نکته مهم) پس در این حالت هم 108طریق می توان شمرد،اگر A سه عضوی باشه(3)آنگاه B اجتماع Cبه 3طریق می توان انتخاب کرد (نکته مهم) پس در این حالت هم 36طریق می توان شمرد و اگرAبرابرD باشه این هم یک طریق می باشد در نهایت حالت چهارم به252 طریق می باشد
حالت پنجمD تهی باشه آنگاه برای A صفر تا 4 عضوی اتفاق می افتد که به ترتیب انتخاب A. برابر 1 بعدی 4 بعدی 6 بعدی 4 و 1می باشه که با همان ترتیب برای Bاجنماع C داریم 81 بعدی 27 بعدی 9 بعدی 3 و 1 می باشد در نتیجه تعداد حالت پنجم برابر است با
$$
1×81+4×27+6×9+4×3+1×1 =256
$$
مجموع 5 حالت برابر
$$
1+16+61+252+256=589
$$