یک خط با نوشتن معادله اش مشخص می شود. معادله ی خط قائم بر منحنی $f$ در نقطه $(a,f(a))$ برابر است با $$y-y_0=m'(x-a)$$
که در آن $m'=-\frac{1}{f'(a)}$ .
در معادله دایره یا به طور کلی معادلات ضمنی که می توان به صورت $f(x,y)=0$ نمایش داد با استفاده از مشتق گیری ضمنی باید شیب خط مماس$m$ را پیدا کنید و از آنجا شیب خط قائم$m'=-\frac1{m}$ را بیابید.
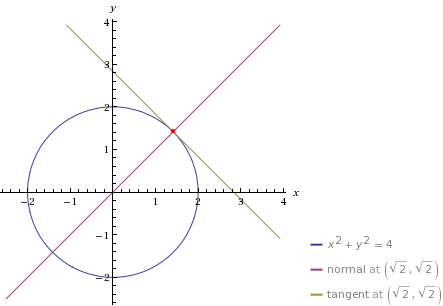
مثلا برای معادله خط قائم بر دایره $x^2+y^2=4$ در نقطه $(\sqrt 2,\sqrt 2)$ ابتدا با مشتق گیری ضمنی داریم:
$$2x+2y'y=0$$ لذا $m=y'=\frac{-2x}{2y}\mid_{(\sqrt2,\sqrt2)}=-1$ و $m'=1$
و معادله خط قائم برابر است با:
$$y-\sqrt 2=1(x-\sqrt2)$$