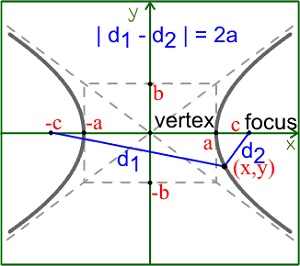
طبق تعریف، هذلولی مکان هندسی مجموعه نقاطی است از صفحه که تفاضل فاصله هر نقطه روی آن از دو نقطه به نام کانون مقداری است ثابت. یعنی با توجه به شکل بالا:
$$d_1-d_2=2a$$
زمانی که محور اصلی محور افقی باشد کانون ها در نقاط $(-c,0)$ و $(c,0)$ قرار دارند.
حال فرض کنید $d_1$ فاصله نقطه $(x,y)$ روی هذلولی از کانون $(-c,0)$ باشد که باتوجه به فرمول فاصله دو نقطه میتوان نوشت:
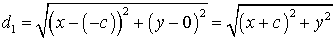
به همین صورت اگر $d_2$ فاصله همان نقطه از کانون $(c,0)$ باشد میتوان نوشت:
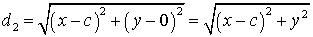
حال با توجه به تعریف هذلولی و دو رابطه ای که در بالا نوشتیم تعریف میکنیم:
$$d_1=c+a$$ و همچنین $$d_2=c-a$$ پس خواهیم داشت:
$$d_1-d_2=(c+a)-(c-a)=2a$$
پس برای هر نقطه $(x,y)$ روی هذلولی خواهیم داشت:$$d_1-d_2=2a$$
حالا که ما رابطه تفاضل فاصله ها را بلدیم، بدنبال معادله ی هذلولی میگردیم:
با $d_1-d_2=2a$ شروع میکنیم و از 2 رابطه ای که در ابتدا برای فاصله ها بدست آوردیم کمک میگیریم(با فرض اینکه $d_1>d_2$)و با جایگذاری آنها خواهیم داشت:
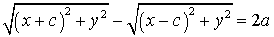
برای خلاص شدن از شر رادیکالها $2a$ را به سمت راست منتقل کرده و طرفین تساوی را به توان دو میرسانیم داریم:
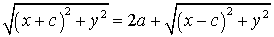
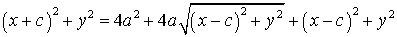
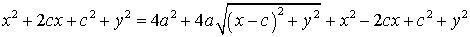
با ساده کردن طرفین خواهیم داشت:
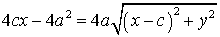
و با تقسیم طرفین بر 4 خواهیم داشت:
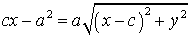
مجدد طرفین را به توان دو میرسانیم تا از شر رادیکال خلاص شویم پس داریم:
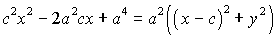
با بسط دادن $(x-c)^2$ و ضرب $a^2$ در پرانتز خواهیم داشت:
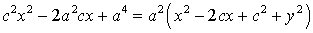
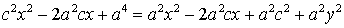
حال تمام متغیرها را به یک سمت و ثابت ها را به سمت دیگر تساوی برده خواهیم داشت:
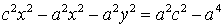
با فاکتور گیری از $x^2$ در سمت چپ و $a^2$ در سمت راست خواهیم داشت:
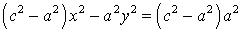
توجه داریم که در هر دو سمت تساوی عبارت $c^2-a^2$ موجود است. تعریف میکنیم
$c^2-a^2=b^2$ و آنرا جایگزین میکنیم خواهیم داشت:
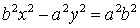
در نهایت با تقسیم طرفین بر $a^2b^2 $ به معادله ی مربوط به هذلولی میرسیم یعنی:
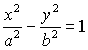
که این معادله فرم استاندارد مهادله هذلولی خواهد بود و همچنین رابطه فیثاغورث $c^2=a^2+b^2$ را در اختیر ما قرار میدهد.