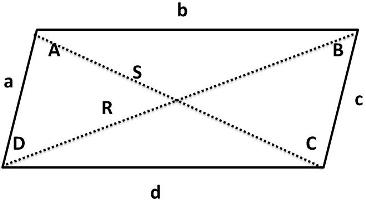
قانون کسینوسها را می نویسیم:
$$ R^{2} = a^{2} + b^{2} -2abcos(A)$$
$$ R^{2} = c^{2} + d^{2} -2cdcos(C)$$
$$ S^{2} = c^{2} + b^{2} -2cbcos(B)$$
$$ S^{2} = a^{2} + d^{2} -2adcos(D)$$
اگر دو رابطه اول را در نظر بگیریم طرف اول هر دو برابر است لذا طرفهای دوم نیز برابر هستند داریم:
$$a^{2} + b^{2} -2abcos(A)=c^{2} + d^{2} -2cdcos(C) \Rightarrow $$
$$a^{2} + b^{2}-c^{2} - d^{2}=2abcos(A)-2cdcos(C) $$
بطور مشابه از دو رابطه آخر داریم:
$$a^{2} + b^{2}-c^{2} - d^{2}=2adcos(D) -2cbcos(B) $$
که طرف اول هر دو برابر هستند لذا طرف های دوم هم برابر هستند لذا داریم:
$$2abcos(A)-2cdcos(C)= 2adcos(D) -2cbcos(B) \Rightarrow $$
$$2abcos(A)+2cbcos(B)= 2adcos(D)+2cdcos(C) \ \ \ \ \ \ \ (1)$$
حال طرفین 4 رابطه ی اولیه را اگر باهم جمع کنیم خواهیم داشت:
$$2a^{2} +2 b^{2}+2c^{2} +2d^{2}$$
$$-2abcos(A)-2cdcos(C)-2cbcos(B) -2adcos(D)$$
$$=2R^{2}+2 S^{2}$$
حال اگر فرض مساله را بکار ببریم خواهیم داشت:
$$-2abcos(A)-2cdcos(C)-2cbcos(B) -2adcos(D)=0$$
و حال با بکار بردن رابطه ی $(1)$ داریم:
$$ 4abcos(A)+4cbcos(B)=0 \Rightarrow 4b(acos(A)+ccos(B))=0$$
و این یعنی $ acos(A)+ccos(B)=0 $ به طور مشابه $ acos(D)+ccos(C)=0$
حال داریم:
$$- \frac{a}{c}= \frac{cos(B)}{cos(A)} $$
$$- \frac{a}{c}= \frac{cos(C)}{cos(D)} $$
لذا داریم:
$$cos(B)cos(D)=cos(A)cos(C) \Rightarrow 2cos(B)cos(D)=2cos(A)cos(C) \Rightarrow $$
$$cos(B+D)+cos(B-D)=cos(A+C)+cos(A-C)$$
اما از اینکه $A+B+C+D=360$ داریم:$ cos(B+D)=cos(A+C) $ پس با حذف از طرفین داریم:$cos(B-D)= cos(A-C) $
پس با توجه به اینکه زاویه ها بین صفر تا 180 درجه و مثبت هستند داریم که باید $B-D=A-C$ یعنی
$A+D=B+C$ و چون مجموع زوایا 360 است لذا $A+D=B+C=180$
یا
$B-D=C-A$ یعنی
$A+B=D+C$ و چون مجموع زوایا 360 است لذا $A+B=D+C=180$