بنابر شکل زیر و مفروضات مساله چنانچه $V$ حجم آب داخل مخروط باشد در اینصورت $V'_t=3$ . ما میخواهیم $y'_t$ را بیابیم.
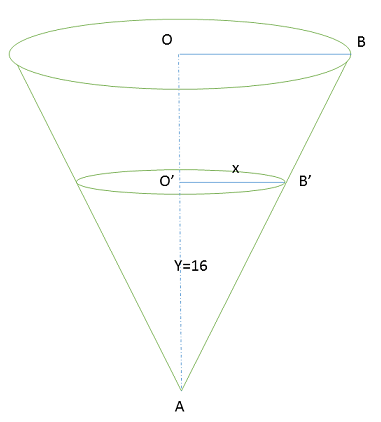
بنابر قضیه تالس $\frac{O'A}{OA}=\frac{x}{4}$ بنابراین $\frac{y}{24}=\frac x4$ و لذا $4y=24x$ و لذا $y'_t=6x'_t$
از طرفی $\frac{O'A}{OA}=\frac{O'B'}{OB}$ بنابراین $\frac {16}{24}=\frac x4$ و لذا $ x=\frac 83 $
حال با توجه به $V=\frac 13\pi x^2y$ داریم
$$ V'_t=\frac 23\pi xx'_ty+\frac 13\pi x^2y'_t $$
با جاگذاری موارد فوق در رابطه اخیر داریم
$$3=\frac 23\pi \frac 83\frac 16y'_t(16)+\frac 13\pi (\frac 83)^2y'_t$$
که از آن $y'_t$ به دست می آید.