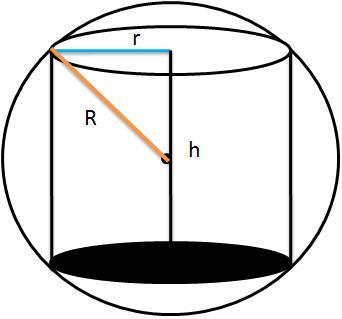
ابتدا رابطه ی بین $r $ و $h $ را می یابیم که به کمک فیثاغورث داریم:
$$ R^{2} = r^{2} +( \frac{h}{2} )^{2} \Rightarrow h^{2}=4(R^{2} - r^{2}) \Rightarrow h=2 \sqrt{R^{2} - r^{2}} $$
اما همانطور که گفته شده $ S=2\pi h r $ و به جای $ h $ از رابطه بدست آمده استفاده می کنیم سپس ماکزیمم تابع را می یابیم.
$S=4\pi r \sqrt{R^{2} - r^{2}} \Rightarrow S'=4\pi \sqrt{R^{2} - r^{2}}-4\pi r \times \frac{r}{\sqrt{R^{2} - r^{2}}} =$
$S'= \frac{4\pi R^{2}-8\pi r^{2} }{\sqrt{R^{2} - r^{2}}} $
باید نقطه ای که مشتق صفر است را بیابیم:
$$4\pi R^{2}-8\pi r^{2}=0 \Rightarrow R^{2}=2r^{2} \Rightarrow r= \frac{ \sqrt{2} }{2}R $$