نسبت ارتفاع به شعاعِ قاعدهٔ یک استوانه چقدر باشد تا مساحت رویهٔ جانبی استوانه بیشنه شود زمانی که این استوانه در یک کرهٔ ثابت محاط شده است؟

Question

می‌خواهیم یک استوانه مستدیر قائم را در یک کره به شعاع مفروض محاط کنیم. نسبت ارتفاع به شعاع قاعده استوانه چه قدر باشد تا مساحت رویه جانبی استوانه حداکثر ممکن باشد؟

Answer 1

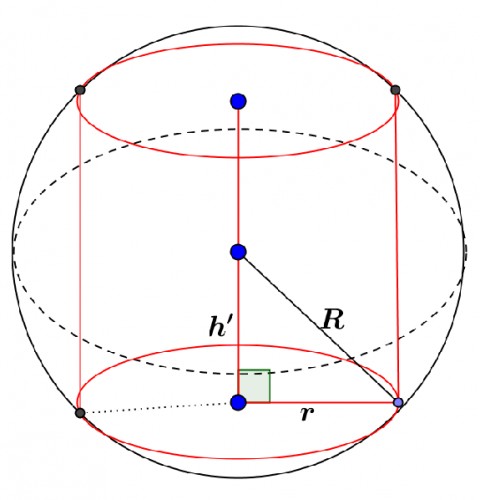
اگر ارتفاع استوانه را $h$ بنامیم که $h=2h'$ درمثلث قائم الزاویه بنابه فیثاغورس در تصویر داریم: $r= \frac{ \sqrt[]{4R^2-h^2} }{2} $

مساحت رویه جانبی استوانه برابر است با:$s=2 \pi rh= \pi h \sqrt{4R^2-h^2} $

$s'_{h} =\pi \sqrt{4R^2-h^2}- \frac{\pi h^2}{\sqrt{4R^2-h^2}}=\frac{\pi[ 4R^2-2h^2]}{\sqrt{4R^2-h^2}}=0 $

درنتیجه $h=\sqrt{2}R$ و $r= \frac{\sqrt{2}}{2} R$

وبه این ترتیب :

$ \frac{h}{r}= \frac{\sqrt{2}R}{\frac{\sqrt{2}}{2} R}=2 $

Comments

Khode_M2@ پاسخ به سوال مورد نظرتان هست؟

---

@good4us ممنون از وقتی که گذاشتی دوست عزیز. منتها بنده متوجه نمیشم چجوری از فیثاغورس استفاده کردی که r برابر همچین عبارتی شده!

---

Khode_M2@ خب درمثلث قائم الزاویه $r^2=R^2-h'^2$ شما به جای $h'$ مساوی آن $\frac{h}{2}$را قرار دهید  و با مخرج مشترک گیری و ریشه گیری به نتیجه می رسید

---

Khode_M2@به این صورت:$r^2=R^2-\frac{h^2}{4}$ می توانیم بنویسیم $r^2=\frac{4R^2-h^2}{4}$ باریشه گیری
$ r= \frac{ \sqrt{4R^2-h^2} }{2} $

---

@Khode_M2 آقای @good4us زحمت کشیدند و در دیدگاه به پرسش‌تان پاسخ دادند. آیا مشکل‌تان رفع شد؟ اگر بلی از تیک تأیید سمت راست پاسخ و سه‌گوش‌های رو به بالای سمت راست پاسخ و دیدگاه‌ها برای امتیاز دادن استفاده کنید.