اصول موضوعه هیلبرت به پنج دسته تقسیم می شوند: وقوع، بینیبت، همنهشتی، پیوستگی و توازی.
یکی از اصول همنهشتی همان ملاک (ض ز ض) برای مثلث ها است.(یعنی به عنوان یک اصل پذیرفته شده و اثبات نمیکینم.)
حالت های (ز ض ز) و (ض ض ض) را می توان اثبات کرد.
در مورد سوال بعدی حالتی که دو ضلع و زاویه غیر بین باشد هم نهشتی نتیجه نمی شود زیرا اگر مثلث دلخواه $ABC$را در نظر بگیرید و به مرکز $B$ و شعاع $AB$ کمانی بزنید تا امتداد $AC$ را در نقطه $D$ قطع کند:
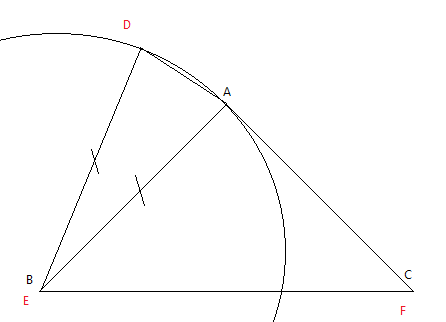
در اینصورت در دومثلث $ABC$ و $DEF$ داریم $AB=DE$ و $EF=BC$ و $\angle F=\angle C$ یعنی حالت دو ضلع و زاویه غیر بین است ولی مثلث ها هم نهشت نیستند. پس دو ضلع و زاویه غیر بین همنهشتی را نتیجه نمیدهد.
ولی دو زاویه و ضلع غیر بین هم نهشتی را نتیجه میدهد زیرا اگر دوزاویه از مثلثی با دو زاویه از مثلث دیگر برابر باشند در اینصورت زاویه سوم آنها هم برابر خواهد بود و به حالت دو زاویه و ضلع بین (ز ض ز) تبدیل خواهد شد.