خوب خودتون جواب خودتون رو دادید تقریبا.
اگر به این سوال و جواب هایی که داده شده نگاه کنید گفتیم که برای مثلا $2^\sqrt 2$ ابتدا دنباله ای در نظر میگیریم از اعداد گویا که به $\sqrt 2$ همگرا باشد.
این دنباله از جمله میتونه دنباله بسط اعشاری $\sqrt 2$ باشه. یعنی
$$r_n=1, 1.4, 1.41, 1.414,...2^\sqrt 2$$
بنابراین اگر بخواهیم $ 2^\sqrt 2 $ را تخمین بزنیم در اینصورت کافی است دنباله $2^{r_n}$ رو در نظر بگیرید
اگر جمله اول تقریب رو در نظر بگیرید خواهیم داشت $2^1=2$
اگر جمله دوم تقریب را در نظر بگیرید خواهیم داشت $2^{1.4}=2^{\frac {14}{10}}=2.639.2$
اگر جمله سوم را در نظر بگیریم در اینصورت $2^{1.41}=2^{\frac{141}{100}}=2.65737$
و به همین ترتیب می توانیم ادامه دهیم. مقدار $2^\sqrt 2$ برابر است با $ 2.66514...$
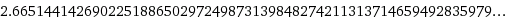
پس اگر توجه کنید کافی است که ما بلد باشیم ریشه های $n$ ام یک عدد رو بدست بیاریم. که الگوریتم کلی هم برای اینگونه مواقع وجود دارد(اینجا رو نگاه کنید). در واقع برای هر عدد حقیقی $A>0$ مقدار $\sqrt[n]A$ از دنباله زیر به دست می آید:
$$x_{k+1}=\frac 1n((n-1)x_k+\frac{A}{x_k^{n-1}})$$
که در اینجا باید $x_0$ یک حدس اولیه باشد.