مساحت مثلث را با داشتن طول میانه ها به دست آورید

Question

اگر $m_{a} $ و $m_{b} $ و $m_{c} $ طول میانه های مثلث ABC باشد ، آنگاه ثابت کنید که مساحت این مثلث برابر است با :

$$S_{ABC}= \frac{4}{3} \sqrt{p(p-m_{a})(p-m_{b})(p-m_{c} )} $$

که در آن $p = \frac{1}{2}(m_{a}+m_{b}+m_{c})$

Answer 1

ممکنه هر کسی با دید متفاوتی به این مساله نگاه کنه ولی همونطور که واضحه بنابر قاعده هرون مساحت مثلث با اضلاع $m_a, m_b, m_c$ برابر است با $$S_{m_am_bm_c}=\sqrt{p(p-m_a)(p-m_b)(p-m_c)}$$ که $$p=\frac{m_a+m_b+m_c}2$$

پس حالا کافی است ثابت کنید نسبت مساحت مثلث $ABC$ به مثلث با اضلاع $m_a, m_b, m_c$ برابر است با $\frac 43$ .

برای این کار هم مثلا میتونید مثل زیر عمل کنید:

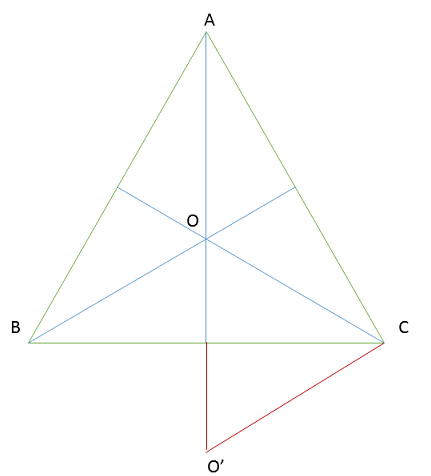
اگر $O$ محل تلاقی میانه ها باشند نقطه $O'$ را قرینه ی نقطه ی $O$ نسبت به پاره خط $BC$ در نظر بگیرید. در اینصورت کافی است توجه کنید که $CO=\frac 23m_c$ و $ OO'=\frac 23 m_a $ و $O'C=\frac 23 m_b$ (چرا؟)

بنابراین $\frac{S_{COO'}}{S_{m_am_bm_c}}=\frac 49$ .

اما $S_{COO'}=\frac 13 S_{ABC}$ ( زیرا در هر مثلث میانه ها مثلث را به شش مثلث با مساحت مساوی تقسیم میکنند(چرا؟))

بنابراین $S_{ABC}=3\times \frac 49S_{m_am_bm_c}=\frac 43S_{m_am_bm_c}$

Comments

سلام Smambmc دقیقا کدوم مساحت میشه؟

---

@Hjkla6000
مساحت مثلث با طول اضلاع $m_a$ و $m_b$ و $m_c$

Answer 2

شکل فوق مثلثی را نشان می‌دهد که خطوط قرمز میانه‌های آن است. اگر از نقطه M خطی به وسط ضلع OB رسم کنیم طبق قضیه تالس در مثلث ABO نتیجه می‌گیریم که خط MN موازی با AO است و طول این خط برابر با یک سوم میانه ma است. طول ضلع‌ ON یک سوم میانه mb و طول ضلع‌ OM یک سوم میانه mc است. از طرفی مساحت مثلث سبز رنگ برابر با یک ششم مساحت کل است. فضیه هرون را برای محاسبه مساحت مثلث سبز رنگ می‌نویسم و حاصل را در شش ضرب می‌کنیم تا مساحت کل بدست آید که نتیجه آن برابر است با: