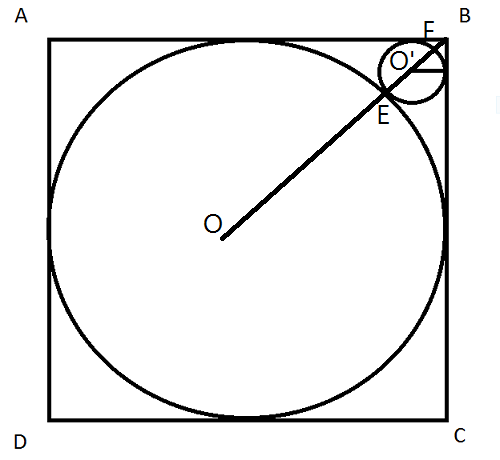
در حالت کلی فرض کنیم که طول ضلع مربع $a$ باشد. در اینصورت قطر مربع برابر است با $a\sqrt{2}$ و لذا $$OB=\frac{a\sqrt 2}{2}$$
اما از طرفی شعاع دایره بزرگ برابر است با $$OE=\frac a2$$
با تقسیم دو رابطه اخیر داریم $$\frac{OB}{OE}=\sqrt 2$$
با استدلال مشابه برای دایره ی کوچک داریم $$\frac{O'B}{O'F}=\sqrt 2$$
حال دقت کنید که
$$\begin{align}O'B&=EB-EO'\\
&=(OB-OE)-EO'\\
&=\frac a2(\sqrt 2-1)-EO'\\
&=\frac a2(\sqrt 2-1)-O'F\end{align}$$
با تقسیم طرفین معادله بالا بر $O'F$ داریم:
$$\sqrt 2=\frac{O'B}{O'F}=\frac{a(\sqrt 2-1)}{2O'F}-1$$
بنابراین $$O'F=\frac{a(\sqrt 2-1)}{2(\sqrt 2+1)}$$