(توجه : دوستان عزیز و گرامی قبل از مطالعه راه حل توجه نمایید که این راه حل مختص بنده است و استفاده از آن در سایت , وبلاگ یا جای دیگری با اسم اینجانب قانونی و شرعی است . امیدوارم که برایتان مفید بوده و مورد استفاده شما قرار گیرد . با تشکر و همچنین آرزوی موفقیت و سربلندی برای شما )
فرض کنیم مثلث متساوی الاضلاعی به طول ضلع $n$ داریم که هر ضلع آن را به $n$ قسمت مساوی تقسیم کرده ایم سپس از هر یک از این نقاط دو پاره خط به موازات دو ضلع دیگر رسم می کنیم تا یک شبکه مثلثی ایجاد شود . به عنوان مثال برای $n=3 $ شکل حاصل به صورت زیر است :
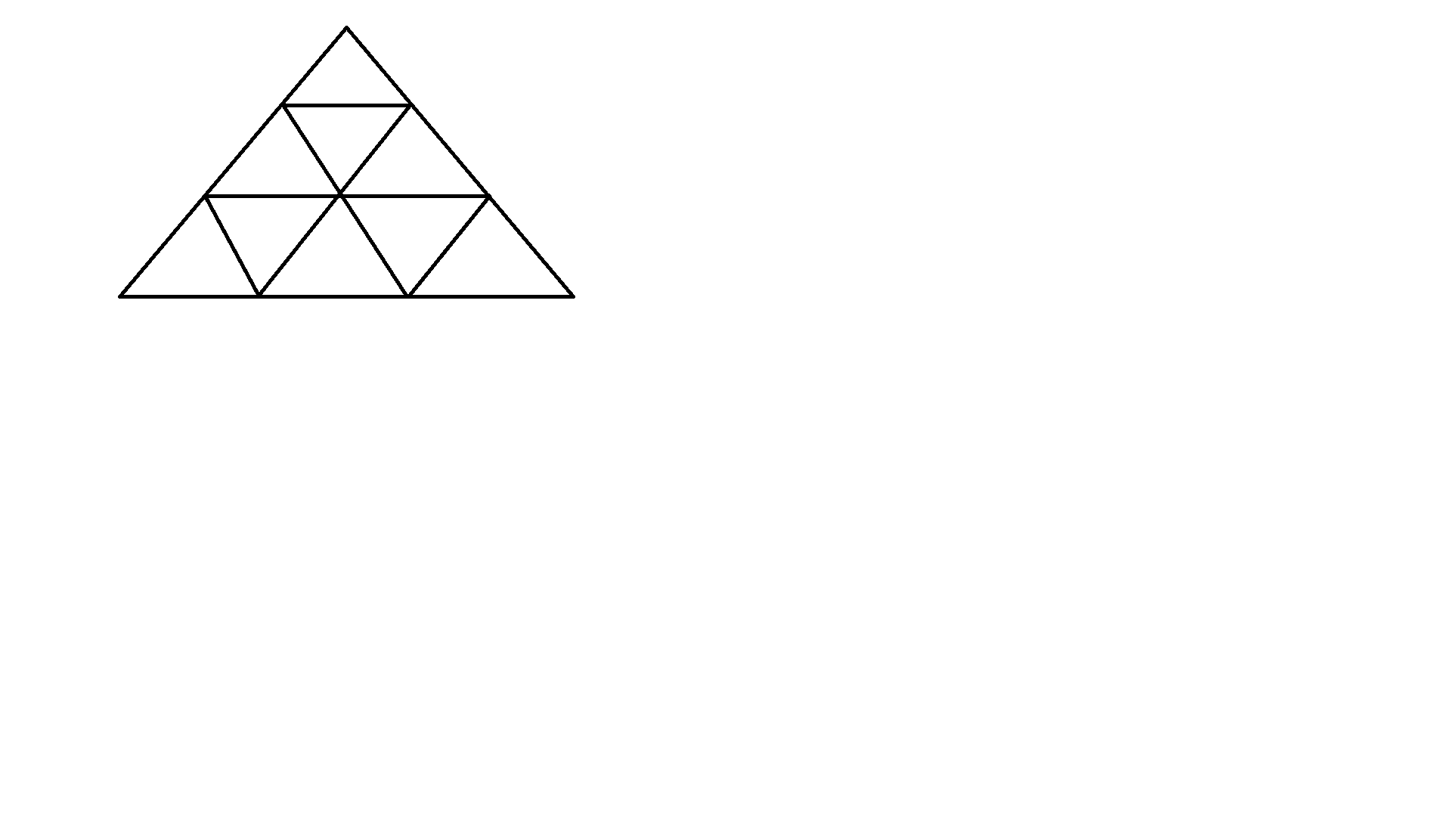حال سوال این است که در شبکه مثلثی که طول هر ضلع آن $n$ است چند مثلث وجود دارد ؟
حل : فرض کنیم شبکه مثلثی داریم که طول هر ضلع آن $n$ است . آنرا $ABC$ می نامیم . به طوری که ضلع $BC$ قاعده آن است . و $A$ راس بالایی آن می باشد . ابتدا تعداد مثلث هایی را می شماریم که قاعده آنها موازی $BC$ می باشد و راس آنها ( نوک مثلث ) به سمت بالاست . تعداد این مثلث ها را با نماد $ \Delta (n)$ نشان می دهیم . فرض کنیم مثلث $ABC$ به صورت زیر است :
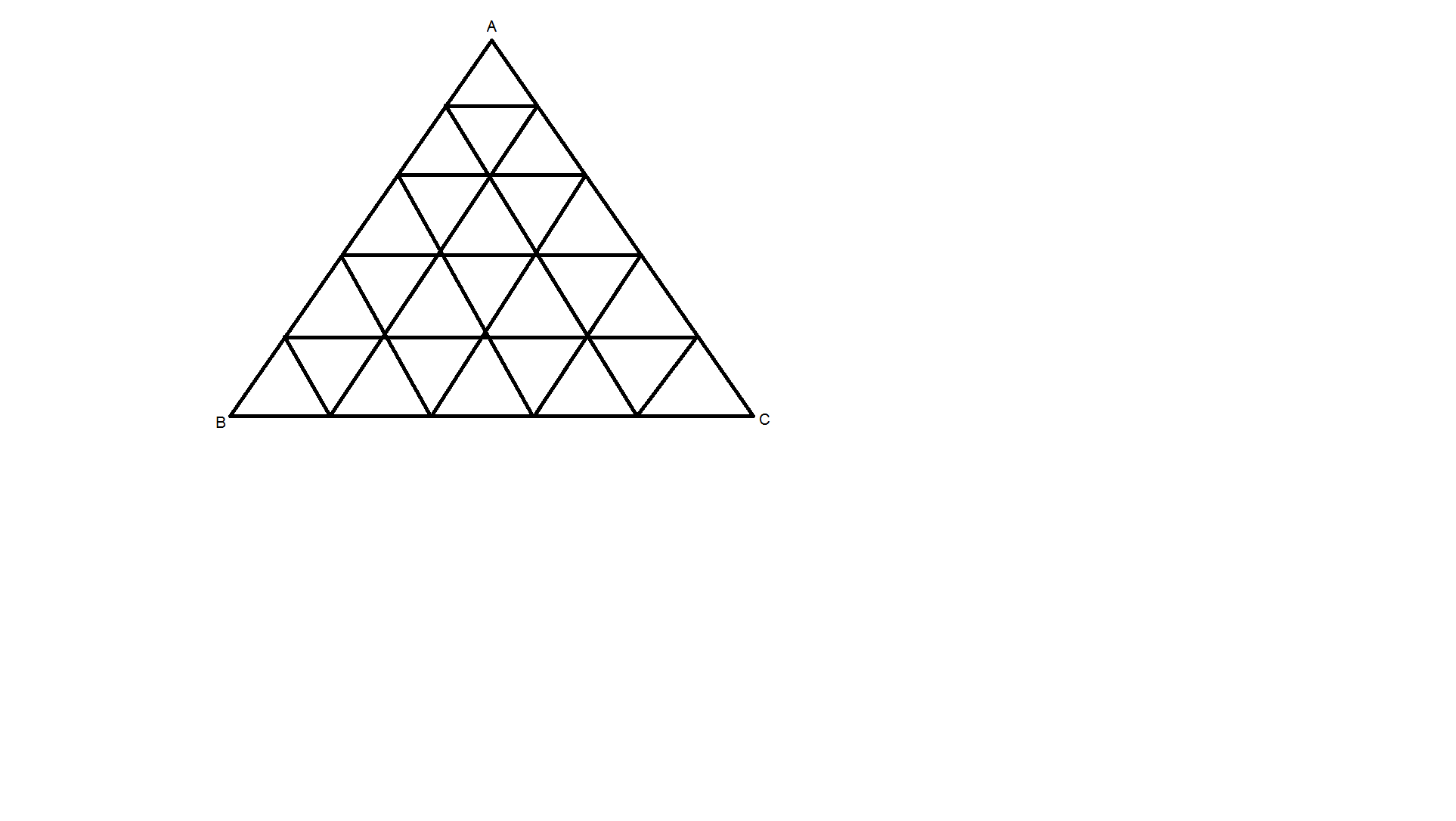
حال دو ضلع $AB$ و $AC$ را به اندازه یک واحد امتداد می دهیم تا به شکل زیر تبدیل شود :
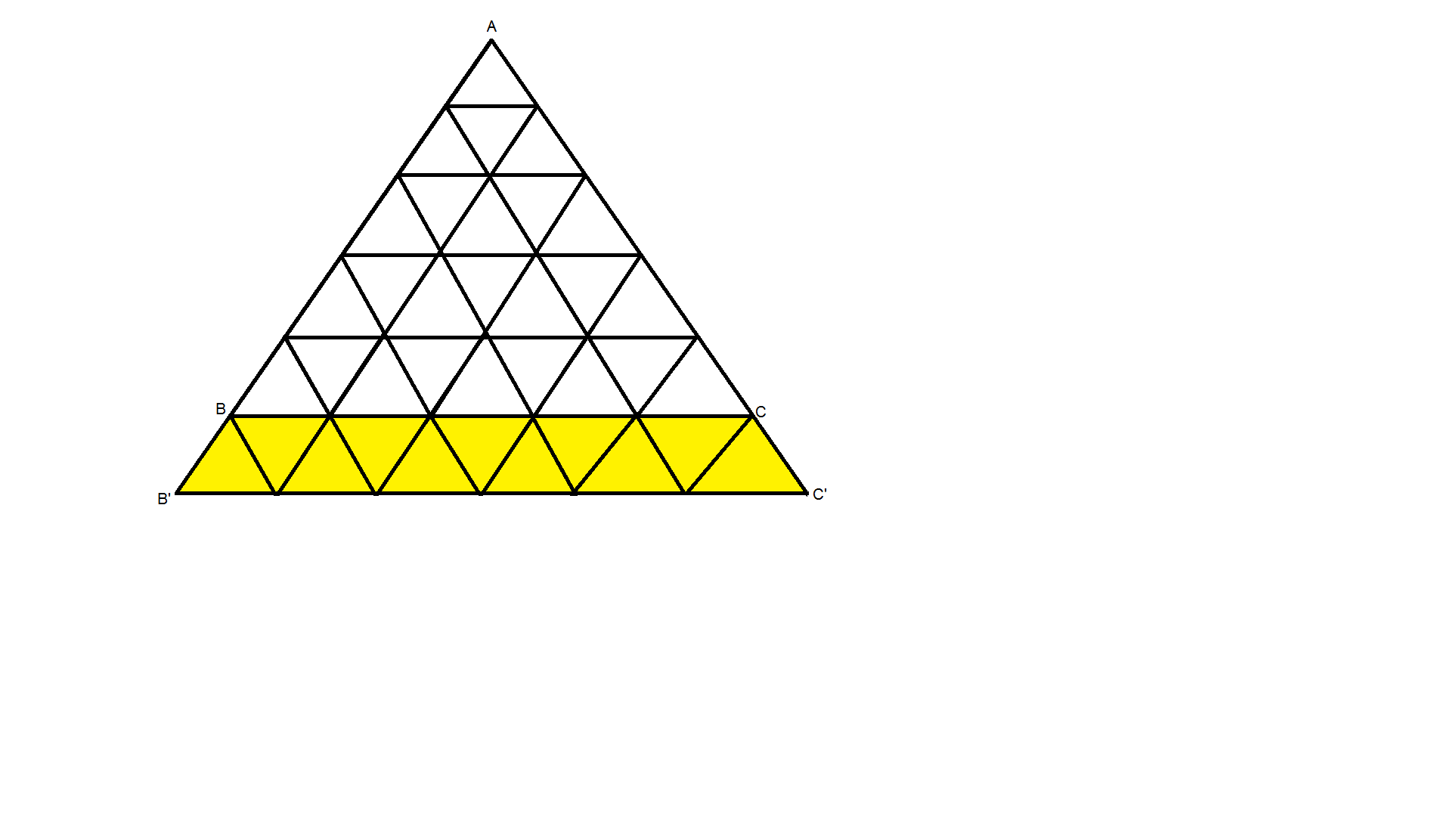
حال هر مثلث در شبکه مثلثی $ABC$ که قاعده آن موازی ضلع $BC$ است و راس آن به سمت بالاست با $3$ نقطه روی قاعده $B'C'$ متناظر است و بعکس . به این صورت که فرض کنید $XYZ$ مثلثی در شبکه مثلثی $ABC $ است که $YZ$ موازی $BC$ است و $X$ و $A$ در یک سمت $YZ$ هستند . حال از راس $Y$ خطی به موازات ضلع $AB$ رسم می کنیم تا پاره خط $B'C'$ را در نقطه ای قطع کند و آنرا $P$ می نامیم . سپس از راس $Z$ دو خط به موازات ضلع $ AC $ و ضلع $AB$رسم می کنیم تا پاره خط $B'C'$ را در دو نقطه قطع کنند و آن دو نقطه را $Q, R$ می نامیم . به شکل زیر توجه نمایید :
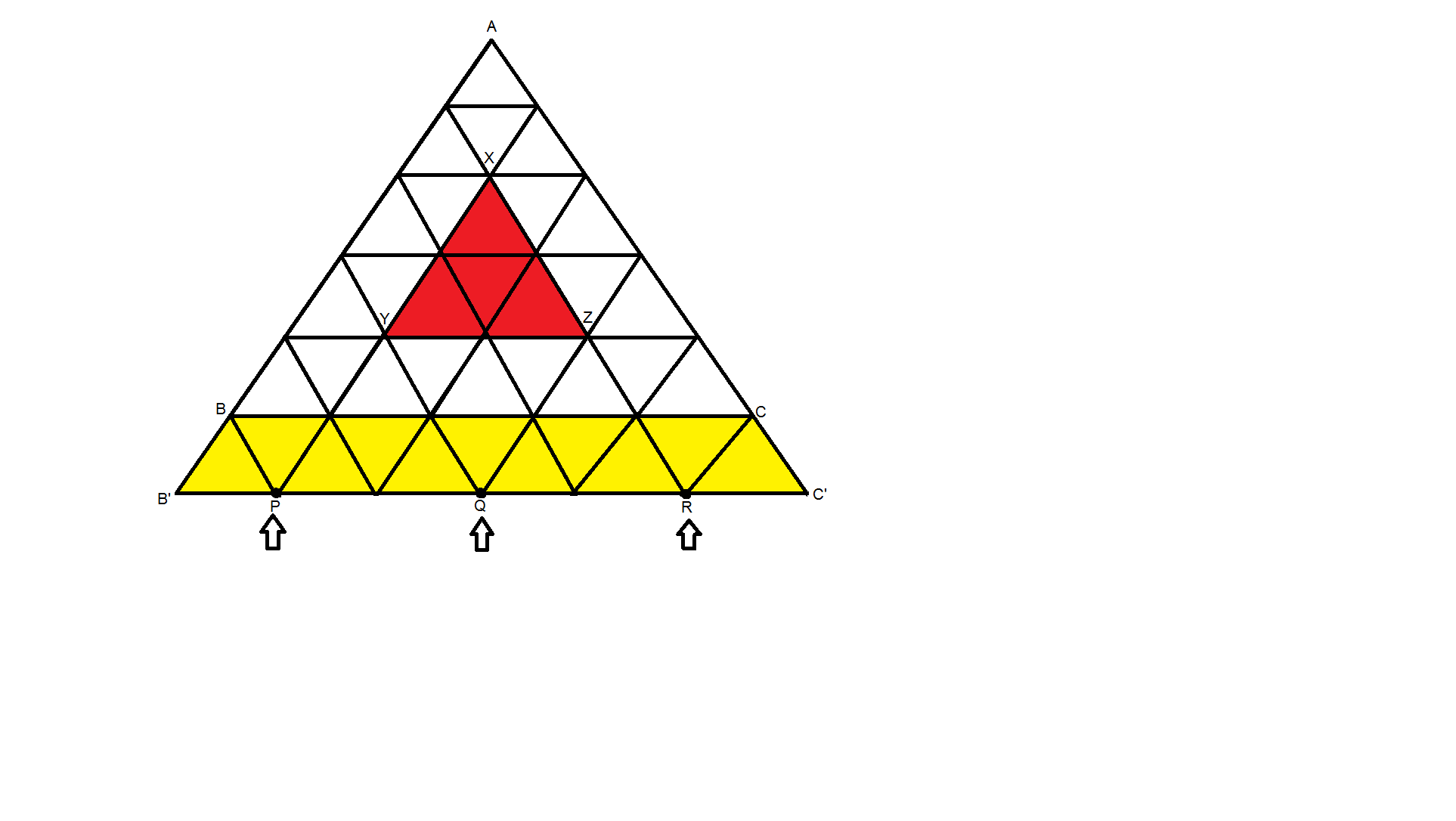
پس نقاط $P,Q,R$ روی پاره خط $B'C'$ متناظر با مثلث $XYZ$ هستند . این یک تناظر یک به یک بین مثلث های شبکه مثلثی که قاعده آنها موازی ضلع $BC$ است و راس آنها به سمت بالاست و زیر مجموعه های $3$ عضوی از نقاط روی پاره خط $B'C'$ برقرار می کند . پس تعداد چنین مثلث هایی برابر است با تعداد راه های انتخاب $3$ نقطه از نقاط روی پاره خط $B'C'$ . روی پاره خط $B'C' $ , $n+2$ نقطه موجود است پس :
$$ \Delta (n)= \binom{n+2}{3} $$
حال تعداد مثلث هایی را می شماریم که قاعده آنها موازی $BC$ است ولی راس آنها ( نوک مثلث ) رو به پایین است . تعداد این مثلث ها را با نماد $ \sigma (n) $ نمایش می دهیم . در شبکه مثلثی $ABC$به ازای هر مثلث کوچک که طول ضلع آن $1$ است و هیچ یک از اضلاع آن بر اضلاع مثلث $ABC$ منطبق نمی باشد یک نقطه در داخل آن مثلث قرار میدهیم به شکل زیر توجه نمایید :
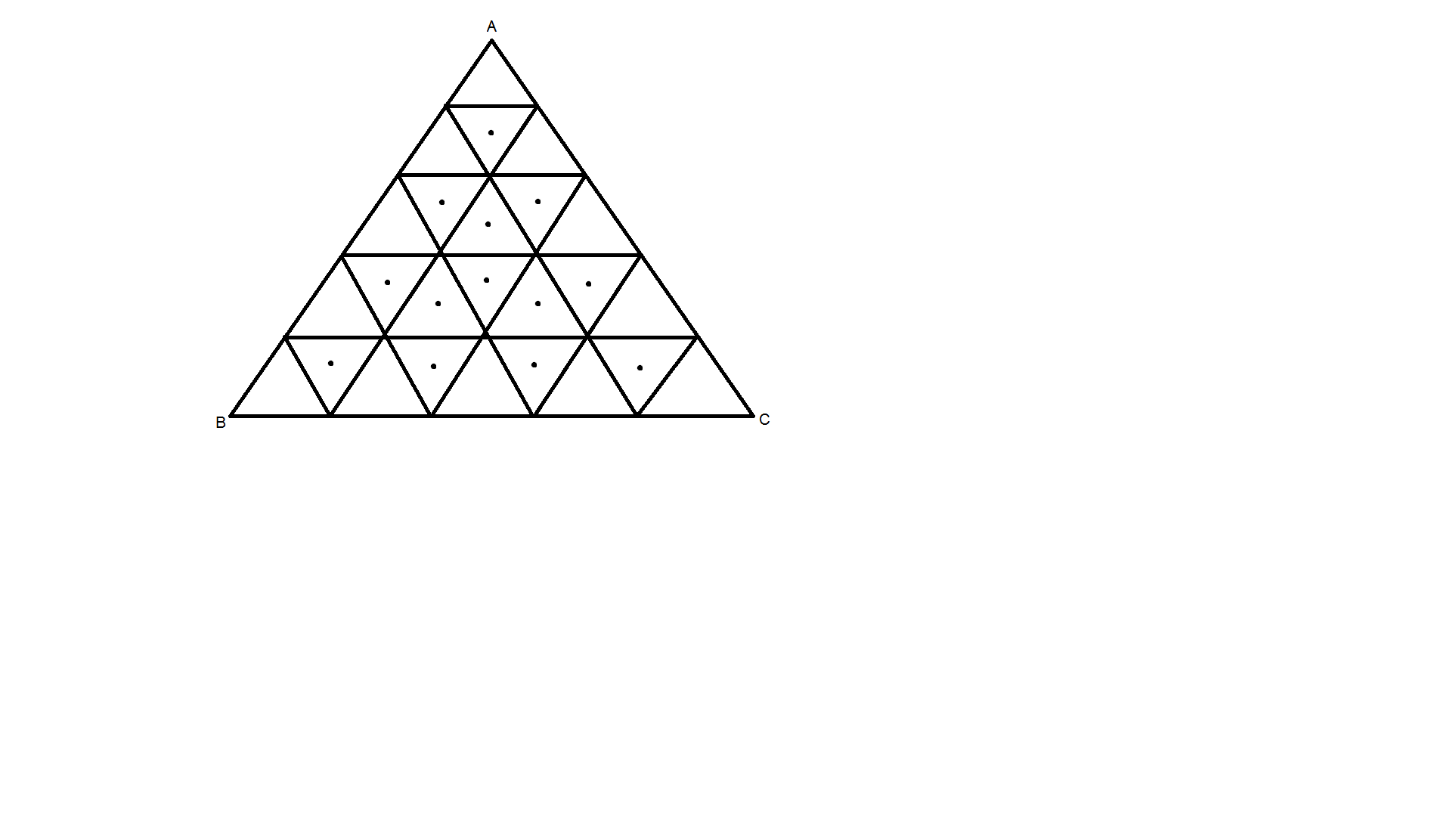
این نقاط را نقاط مرکزی می نامیم .حال هریک از این نقاط متناظر با یک مثلث هستند که قاعده آن موازی ضلع $BC$ است و راس آن ( نوک مثلث ) رو به پایین است . زیرا فرض کنید $XYZ$ مثلثی است که ضلع $YZ$ موازی $BC$ است و راس $X$ و راس $A$ در دو طرف متمایز پاره خط $YZ$ هستند در این صورت مرکز مثلث $XYZ$ منطبق بر یکی از این نقاط است . به شکل زیر توجه نمایید :
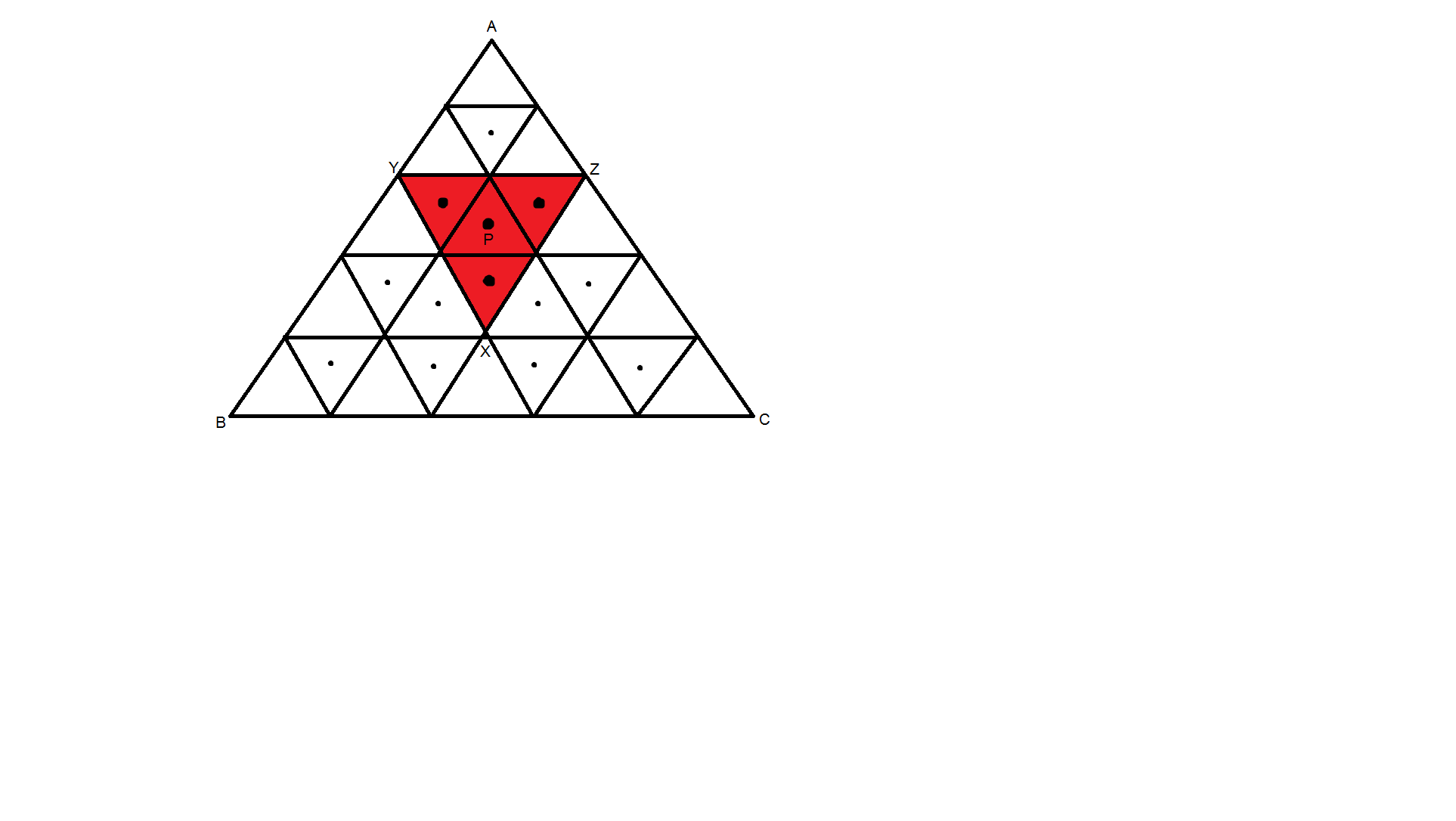
همانطور که در شکل مشاهده می کنید مثلث $XYZ$ متناظر با نقطه $P$ است که در مرکز آن قرار گرفته است . پس تعداد چنین مثلث هایی برابر است با تعداد این نقاط مرکزی . برای شمارش تعداد این نقاط کافی است ابتدا تعداد کل مثلث های کوچک به طول ضلع $1$ را در شبکه مثلثی $ABC$ بشماریم که برابر است با :
$$1+3+...+(2n-1)=n^2$$
حال تعداد مثلث های کوچک به طول ضلع $1$ را که که یک ضلع آنها منطبق بر یکی از اضلاع مثلث $ABC$ می باشد را از آن کم می کنیم که تعداد این مثلث ها برابر است با :
$$n+(n-1)+(n-2)=3n-3$$
پس تعداد نقاط مرکزی در شبکه مثلثی $ABC$ برابر است با :
$$n^2-(3n-3)=n^2-3n+3$$
پس :
$$ \sigma (n)=n^2-3n+3$$
بنابراین تعداد کل مثلث های شبکه مثلثی $ABC$ برابر است با :
$$ \Delta (n)+ \sigma (n)=\binom{n+2}{3}+n^2-3n+3$$
