ЩҮЩ…ЩҲЩҶШ·ЩҲШұ Ъ©ЩҮ Щ…ЫҢШҜЩҲЩҶЫҢШҜ Щ…Ш§ ШҜШұ ЩҮЩҶШҜШіЩҮ Ш§ЩӮЩ„ЫҢШҜШіЫҢ 5 Ш§ШөЩ„ Щ…ЩҲШ¶ЩҲШ№ ЫҢШ§ ШЁЩҶШҜШ§ШҙШӘ ШҜШ§ШұЫҢЩ…:
- ЩҮШұ ШҜЩҲ ЩҶЩӮШ·ЩҮ Щ…ШӘЩ…Ш§ЫҢШІ ЫҢЪ© Ш®Ш· Щ…ЩҶШӯШөШұ ШЁЩҮ ЩҒШұШҜ ШұШ§ Щ…ШҙШ®Шө Щ…ЫҢ Ъ©ЩҶШҜ.
- ЩҮШұ ЩҫШ§ШұЩҮ Ш®Ш· ШұШ§ Щ…ЫҢ ШӘЩҲШ§ЩҶ ШЁЩҮ Ш§ЩҶШҜШ§ШІЩҮ ЩҮШұ ЩҫШ§ШұЩҮ Ш®Ш· ШҜЫҢЪҜШұ ШҜШұ ЫҢЪ© Ш®Ш· ШұШ§ШіШӘ Ш§ШҜШ§Щ…ЩҮ ШҜШ§ШҜ.
- Щ…ЫҢ ШӘЩҲШ§ЩҶ ЫҢЪ© ШҜШ§ЫҢШұЩҮ ШЁШ§ Щ…ШұЪ©ШІ ЩҲ ШҙШ№Ш§Ш№ ШҜЩ„Ш®ЩҲШ§ЩҮ ШұШ§ Щ…ШҙШ®Шө Ъ©ШұШҜ.
- ЩҮЩ…ЩҮ ШІЩҲШ§ЫҢШ§ЫҢ ЩӮШ§ШҰЩ…ЩҮ ЩӮШ§ШЁЩ„ Ш§ЩҶШ·ШЁШ§ЩӮ ЩҮШіШӘЩҶШҜ.
- Ш§ШІ ЩҮШұ ЩҶЩӮШ·ЩҮ ШӘЩҶЩҮШ§ ЫҢЪ© Ш®Ш· ШЁЩҮ Щ…ЩҲШ§ШІШ§ШӘ Ш®Ш· ШҜШ§ШҜЩҮ ШҙШҜЩҮ Щ…ЫҢ ШӘЩҲШ§ЩҶ ШұШіЩ… Ъ©ШұШҜ.
ЩҮЩҶШҜШіЩҮ Ш§ЫҢ Ъ©ЩҮ ШЁШ§ Ш§ЫҢЩҶ Ш§ШөЩҲЩ„ Щ…ЩҲШ¶ЩҲШ№ЩҮ ШіШ§Ш®ШӘЩҮ Щ…ЫҢ ШҙЩҲШҜ ШЁЩҮ ЩҮЩҶШҜШіЩҮ Ш§ЩӮЩ„ЫҢШҜШіЫҢ Щ…ШҙЩҮЩҲШұ Ш§ШіШӘ ЩҲ Щ…ЫҢ ШҜШ§ЩҶЫҢШҜ Ъ©ЩҮ Щ…ЫҢ ШӘЩҲШ§ЩҶЫҢЩ… Ш«Ш§ШЁШӘ Ъ©ЩҶЫҢЩ… Щ…Ш¬Щ…ЩҲШ№ ШІЩҲШ§ЫҢШ§ЫҢ ЩҮШұ Щ…Ш«Щ„Ш« ШЁШұШ§ШЁШұ 180 ШҜШұШ¬ЩҮ Ш§ШіШӘ.
Ш§Щ…Ш§ Щ…Ш§ ЩҮЩҶШҜШіЩҮ ЩҮШ§ЫҢ ШҜЫҢЪҜШұЫҢ ШҜШ§ШұЫҢЩ… Ъ©ЩҮ ШЁЩҮ ЩҮЩҶШҜШіЩҮ ЩҶШ§Ш§ЩӮЩ„ЫҢШҜШіЫҢ Щ…ШҙЩҮЩҲШұЩҶШҜ. ШЁЩҮ Ш№ЩҶЩҲШ§ЩҶ Щ…Ш«Ш§Щ„ ШҜШұ ЩҮЩҶШҜШіЩҮ ЩҮШ°Щ„ЩҲЩ„ЩҲЫҢ( Ъ©ЩҮ ШЁЩҮ Ш¬Ш§ЫҢ Ш§ШөЩ„ ЩҫЩҶШ¬Щ… Ш§ЩӮЩ„ЫҢШҜШі Ш§ШөЩ„ ШҜЫҢЪҜШұЫҢ Ъ©ЩҮ ШЁЩҮ Ш§ШөЩ„ ЩҮШ°Щ„ЩҲЩ„ЩҲЫҢ Щ…Ш№ШұЩҲЩҒ Ш§ШіШӘ Ш§Ш¶Ш§ЩҒЩҮ Щ…ЫҢЪ©ЩҶЫҢЩ…: Ш§ШІ ЩҮШұ ЩҶЩӮШ·ЩҮ ШӯШҜШ§ЩӮЩ„ ШҜЩҲ Ш®Ш· Щ…ЩҲШ§ШІЫҢ ШЁШ§ Ш®Ш· ШҜШ§ШҜЩҮ ШҙШҜЩҮ ШЁШӘЩҲШ§ЩҶ ШұШіЩ… Ъ©ШұШҜ) Щ…ЫҢ ШӘЩҲШ§ЩҶ Ш«Ш§ШЁШӘ Ъ©ШұШҜ Ъ©ЩҮ Щ…Ш¬Щ…ЩҲШ№ ШІЩҲШ§ЫҢШ§ЫҢ ШҜШ§Ш®Щ„ЫҢ ЩҮШұ Щ…Ш«Щ„Ш« Ъ©Щ…ШӘШұ Ш§ШІ 180 Ш§ШіШӘ.(ШЁШұШ§ЫҢ Ш§Ш«ШЁШ§ШӘ ШЁЩҮ ШЁШ®Шҙ ЩҮЩҶШҜШіЩҮ ЩҮШ°Щ„ЩҲЩ„ЩҲЫҢ Ъ©ШӘШ§ШЁ ЩҮЩҶШҜШіЩҮ Ш§ЩӮЩ„ЫҢШҜШіЫҢ ЩҲ ЩҶШ§Ш§ЩӮЩ„ЫҢШҜШіЫҢ ЪҜШұЫҢЩҶШЁШұЪҜ Щ…ШұШ§Ш¬Ш№ЩҮ Ъ©ЩҶЫҢШҜ Ъ©ЩҮ ШҜШұ Ш§ЩҲЩ„ЫҢЩҶ Щ„Щ… Ш§ЫҢЩҶ ШЁШ®Шҙ ЩҲШ¬ЩҲШҜ ЪҶЩҶЫҢЩҶ Щ…Ш«Щ„Ш«ЫҢ Ш§Ш«ШЁШ§ШӘ ШҙШҜЩҮ Ш§ШіШӘ)
ШҜШұ ЩҮЩҶШҜШіЩҮ ШЁЫҢШ¶ЩҲЫҢ( ЩҮЩҶШҜШіЩҮ Ш§ЫҢ Ъ©ЩҮ ШҜШұ ШўЩҶ Ш§ШІ ЩҮШұ ЩҶЩӮШ·ЩҮ ЩҶШӘЩҲШ§ЩҶ ЩҮЫҢЪҶ Ш®Ш·ЫҢ ШЁЩҮ Щ…ЩҲШ§ШІШ§ШӘ Ш®Ш· ШҜШ§ШҜЩҮ ШҙШҜЩҮ ШұШіЩ… Ъ©ШұШҜШӣ ЫҢШ№ЩҶЫҢ ЩҮЫҢЪҶ ШҜЩҲ Ш®Ш· Щ…ЩҲШ§ШІЫҢ ЩҲШ¬ЩҲШҜ ЩҶШҜШ§ШҙШӘЩҮ ШЁШ§ШҙШҜ) Щ…ЫҢ ШӘЩҲШ§ЩҶ Ш«Ш§ШЁШӘ Ъ©ШұШҜ Ъ©ЩҮ Щ…Ш¬Щ…ЩҲШ№ ШІЩҲШ§ЫҢШ§ЫҢ ШҜШ§Ш®Щ„ЫҢ Щ…Ш«Щ„Ш« ШЁЫҢШҙШӘШұ Ш§ШІ 180 Ш§ШіШӘ.
ШҜШұ ШҙЪ©Щ„ ШІЫҢШұ ШЁЩҮ ШӘШұШӘЫҢШЁ ЩҮШҜШіЩҮ ЩҮШ§ЫҢ Ъ©ШұЩҲЫҢШҢ Ш§ЩӮЩ„ЫҢШҜШіЫҢ ЩҲ ЩҮШ°Щ„ЩҲЩ„ЩҲЫҢ ЩҶШҙШ§ЩҶ ШҜШ§ШҜЩҮ ШҙШҜЩҮ Ш§ЩҶШҜ:
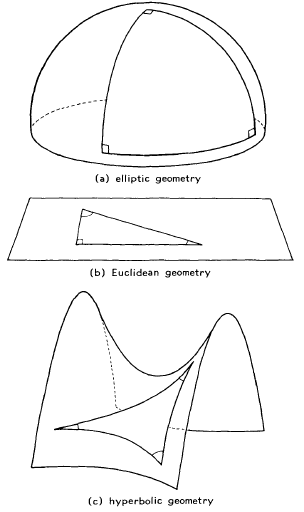
ЫҢЪ© Щ…Ш«Ш§Щ„ Ъ©ЩҮ ШЁЩҮ Ъ©Щ…Ъ© ШўЩҶ Щ…ЫҢ ШӘЩҲШ§ЩҶ ЩҮЩҶШҜШіЩҮ ШЁЫҢШ¶ЩҲЫҢ ШұШ§ ШҜШұЪ© Ъ©ШұШҜ ЩҶЪҜШ§ЩҮ Ъ©ШұШҜЩҶ ШЁЩҮ ЫҢЪ© Ъ©ШұЩҮ Ш§ШіШӘ. Щ…Ш§ ШҜШұ ЩҮЩҶШҜШіЩҮ Ъ©ШұЩҲЫҢ Ш®Ш· ШұШ§ ШҜЩҲШ§ЫҢШұ Ш№ШёЫҢЩ…ЩҮ ШҜШұ ЩҶШёШұ Щ…ЫҢЪҜЫҢШұЫҢЩ…. ЫҢШ№ЩҶЫҢ ШҜШ§ЫҢШұЩҮ Ш§ЫҢ Ъ©ЩҮ Ш§ШІ ШЁШұШ®ЩҲШұШҜ ЫҢЪ© ШөЩҒШӯЩҮ ШЁШ§ ШіШ·Шӯ Ъ©ШұЩҮ Ш§ЫҢШ¬Ш§ШҜ Щ…ЫҢ ШҙЩҲШҜ ШЁЩҮ Ш·ЩҲШұЫҢЪ©ЩҮ ШөЩҒШӯЩҮ Ш§ШІ Щ…ШұЪ©ШІ Ъ©ШұЩҮ ШЁЪҜШ°ШұШҜ. ШҜШұ Ш§ЫҢЩҶШөЩҲШұШӘ ЩҮШұ ШҜЩҲ Ш®Ш·(ЩҮШұ ШҜЩҲ ШҜШ§ЫҢШұЩҮ Ш№ШёЫҢЩ…ЩҮ) ШҜШұ ШҜЩӮЫҢЩӮШ§ ШҜЩҲ ЩҶЩӮШ·ЩҮ ЫҢЪ©ШҜЫҢЪҜШұ ШұШ§ ЩӮШ·Ш№ Щ…ЫҢ Ъ©ЩҶЩҶШҜ.
Щ…Ш«Щ„Ш« Ъ©ШұЩҲЫҢ Ъ©ЩҮ Ш§ШІ ШЁШұШ®ЩҲШұШҜ ШіЩҮ Ш®Ш· ШҜШұ Ъ©ШұЩҮ Ш§ЫҢШ¬Ш§ШҜ Щ…ЫҢ ШҙЩҲШҜ Щ…ЫҢ ШӘЩҲШ§ЩҶ ЩҶШҙШ§ЩҶ ШҜШ§ШҜ Ъ©ЩҮ Щ…Ш¬Щ…ЩҲШ№ ШІЩҲШ§ЫҢШ§ЫҢ Щ…Ш«Щ„Ш« Ъ©ШұЩҲЫҢ ШЁЫҢШҙШӘШұ Ш§ШІ $\pi$ ЩҲ Ъ©Щ…ШӘШұ Ш§ШІ $3\pi$ Ш§ШіШӘ.
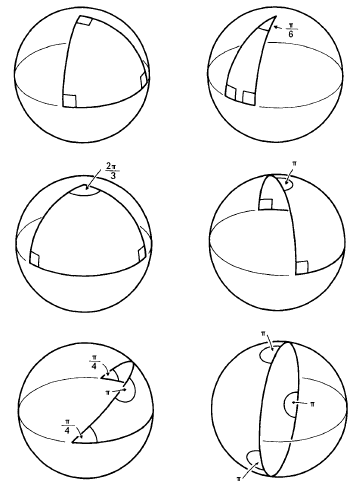
ШЁЩҮ Ш№ЩҶЩҲШ§ЩҶ Щ…Ш«Ш§Щ„ Щ…Ш«Щ„Ш« Ш§ЩҲЩ„ЫҢ Ш§ШІ ШіЩ…ШӘ ЪҶЩҫ ШҜШ§ШұШ§ЫҢ ШіЩҮ ШІШ§ЩҲЫҢЩҮ ЩӮШ§ШҰЩ…ЩҮ Ш§ШіШӘ ЩҲ Ш§Щ„ЫҢ ШўШ®Шұ...
Ш¬Ш§Щ„ШЁЩҮ ШЁЩҮ Ш§ЫҢЩҶ ЩҶЪ©ШӘЩҮ ЩҮЩ… Ш§ШҙШ§ШұЩҮ Ъ©ЩҶЩ… Ъ©ЩҮ ЩҮЩ…ЩҲШ§ШұЩҮ ШЁЫҢЩҶ Щ…ШіШ§ШӯШӘ Щ…Ш«Щ„Ш« Ъ©ШұЩҲЫҢ $\Delta$ ШЁШ§ ШІЩҲШ§ЫҢШ§ЫҢ $A, B , C$ ЩҲ ШҙШ№Ш§Ш№ Ъ©ШұЩҮ $R$ ШұШ§ШЁШ·ЩҮ ШІЫҢШұ ШЁШұЩӮШұШ§Шұ Ш§ШіШӘ:
$$\Delta=R^2((A+B+C)-\pi)$$
Щ…Ш«Щ„Ш§ Щ…Ш«Щ„Ш« Ш§ЩҲЩ„ЫҢ ШЁШ§ ШіЩҮ ШІШ§ЩҲЫҢЩҮ ЩӮШ§ШҰЩ…ЩҮ $\frac 18$ ШіШ·Шӯ Ъ©ШұЩҮ ШұШ§ Ш§ШҙШәШ§Щ„ Ъ©ШұШҜЩҮ ЩҲ ЪҶЩҲЩҶ Ъ©Щ„ Ъ©ШұЩҮ Щ…ШіШ§ШӯШӘЫҢ ШЁШұШ§ШЁШұ $4\pi R^2$ ШҜШ§ШұШҜ ЩҫШі Щ…ШіШ§ШӯШӘ ШўЩҶ ШЁШұШ§ШЁШұ
$$\frac 18(4\pi R^2)=\frac 12\pi R^2=R^2((\frac\pi 2+\frac \pi2+\frac \pi2)-\pi)$$