ابتدا نشان می دهیم :
$$1+2+...+n = \frac{n(n+1)}{2}$$
راه اول :
با استفاده از اتحاد چوشی - چی اثبات می کنیم .
اتحاد چوشی - چی : اگر $n,k$ دو عدد طبیعی باشند آنگاه داریم :
$$ \binom{k}{k} +\binom{k+1}{k}+...+ \binom{n}{k}= \binom{n+1}{k+1} $$
حال قرار دهید $k=1$ داریم :
$$ \binom{1}{1} +\binom{1+1}{1}+...+ \binom{n}{1}= \binom{n+1}{1+1}$$
$$ \Rightarrow \binom{1}{1} +\binom{2}{1}+...+ \binom{n}{1}= \binom{n+1}{2}$$
$$ \Rightarrow 1+2+...+n=\frac{n(n+1)}{2}$$
راه دوم :
فرض کنید $S=1+2+...+n$ داریم :
$$S=1+2+...+(n-1)+n$$
$$S=n+(n-1)+...+2+1$$
$$ \Rightarrow 2S=(1+n)+(2+(n-1))+...+((n-1)+2)+(n+1)$$
$$ \Rightarrow 2S=(n+1)+(n+1)+...+(n+1)+(n+1)$$
$$ \Rightarrow 2S=n(n+1)$$
$$\Rightarrow S=\frac{n(n+1)}{2}$$
راه سوم :
مستطیل $n \times (n+1)$ را در نظر بگیرید و آنرا به مربع های واحد افراز کنید سپس مطابق شکل زیر آنرا به دو قسمت مساوی تقسیم کرده و مربع های یک قسمت را زرد و قسمت دیگر را قرمز کنید :
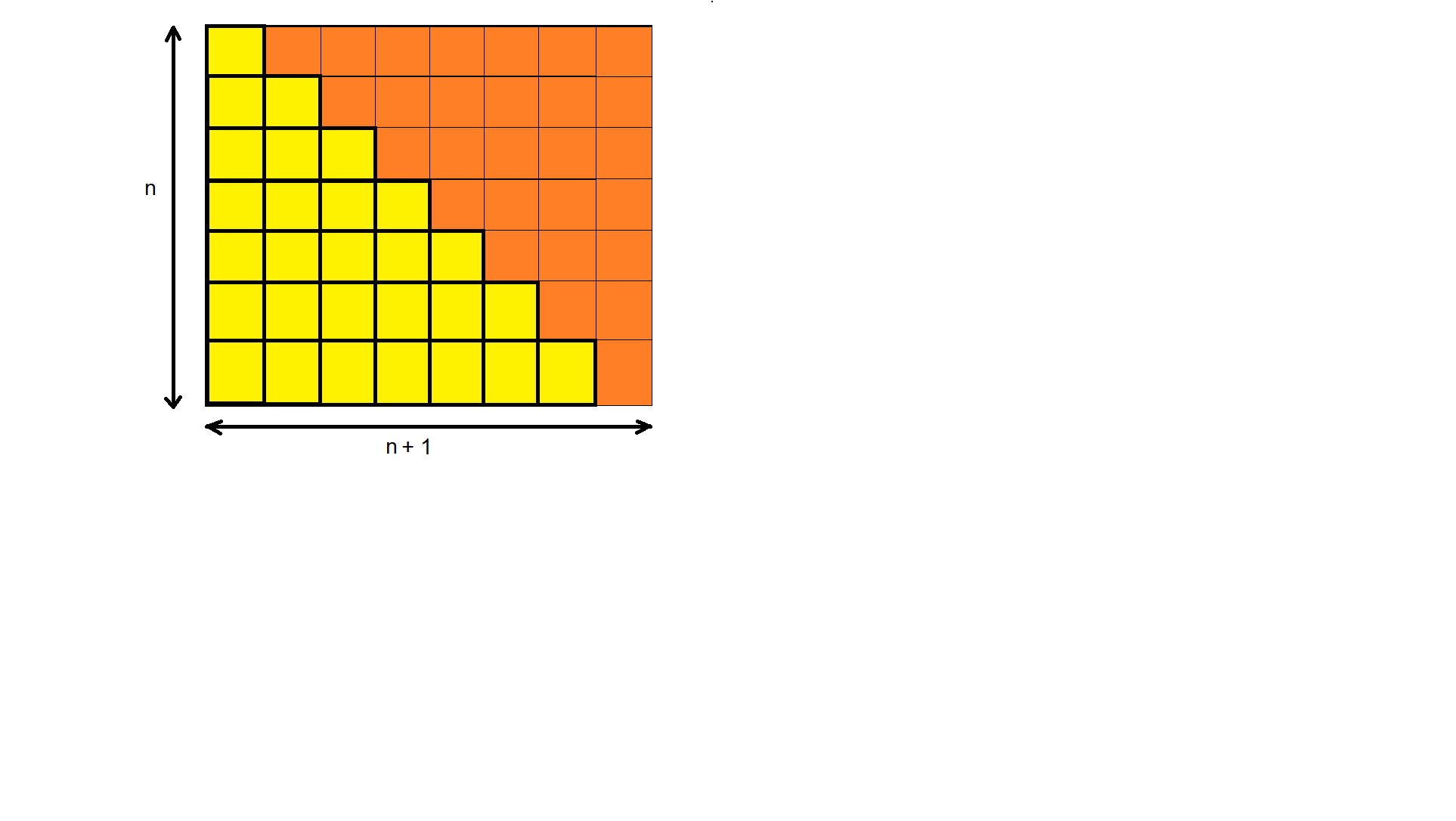
تعداد کل مربع های داخل مستطیل $n \times (n+1)$ برابر $n(n+1)$ است . حال فرض کنید $S_{1}$ تعداد مربع های زرد و $S_{2}$ تعداد مربع های قرمز است در این صورت $ S_{1}= S_{2}$ و همچنین داریم $ S_{1}+ S_{2}=n(n+1) $ . پس :
$$ 2S_{1}=n(n+1)$$
$$ \Rightarrow S_{1}=\frac{n(n+1)}{2}$$
از طرفی طبق شکل بالا تعداد مربع های زرد برابر است با :
$$S_{1}=1+2+...+n$$
پس $ 1+2+...+n = \frac{n(n+1)}{2} $ .
حال نشان می دهیم :
$$1^2+2^2+...+n^2=\frac{n(n+1)(2n+1)}{6}$$
با استفاده از اتحاد چوشی - چی ثابت می کنیم . در اتحاد چوشی - چی قرار دهید $k=2 $ داریم :
$$\binom{2}{2} +\binom{2+1}{2}+...+ \binom{n}{2}= \binom{n+1}{2+1}$$
$$ \Rightarrow \binom{2}{2} +\binom{3}{2}+...+ \binom{n}{2}= \binom{n+1}{3}$$
$$ \Rightarrow \sum_{i=2}^{n} \binom{i}{2} =\binom{n+1}{3}$$
$$\Rightarrow \sum_{i=2}^{n} \frac{i(i-1)}{2} =\frac{(n+1)n(n-1)}{6}$$
$$\Rightarrow \frac{1}{2}\sum_{i=1}^{n} i(i-1)=\frac{(n+1)n(n-1)}{6}$$
$$ \Rightarrow \sum_{i=1}^{n} i^2 - \sum_{i=1}^{n} i =\frac{(n+1)n(n-1)}{3}\ \ \ \star $$
از طرفی در بالا ثابت کردیم $ \sum_{i=1}^{n} i=\frac{n(n+1)}{2} $ پس با جاگذاری در $ \star $ داریم :
$$\Rightarrow \sum_{i=1}^{n} i^2 - \frac{n(n+1)}{2}=\frac{(n+1)n(n-1)}{3}$$
$$\Rightarrow \sum_{i=1}^{n} i^2 =\frac{(n+1)n(n-1)}{3}-\frac{n(n+1)}{2}$$
$$\Rightarrow \sum_{i=1}^{n} i^2 =\frac{n(n+1)(2n+1)}{6}$$
حال در اتحاد چوشی - چی قرار دهید $k=3$ و با استدلالی مشابه استدلال بالا ثابت می شود :
$$1^3+2^3+...+n^3=\frac{n^2(n+1)^2}{4}$$
و اما اثبات اتحاد چوشی - چی :
طبق اتحاد پاسکال می دانیم :
اگر $i,k$ دو عدد طبیعی باشند آنگاه :
$$ \binom{i+1}{k+1} = \binom{i}{k} + \binom{i}{k+1} $$
$$\Rightarrow \binom{i}{k}=\binom{i+1}{k+1}-\binom{i}{k+1}$$
پس :
$$ \sum_{i=k}^n \binom{i}{k}=\sum_{i=k}^n (\binom{i+1}{k+1}-\binom{i}{k+1}) $$
حال طبق قاعده ادغام ( تلسکوپی )داریم :
$$ \sum_{i=k}^n \binom{i}{k} = \binom{n+1}{k+1} - \binom{k}{k+1} $$
$$\Rightarrow \sum_{i=k}^n \binom{i}{k} = \binom{n+1}{k+1}$$