Щ…ШұЪ©ШІ ШҜШ§ЫҢШұЩҮЩ” ШіЩ…ШӘ ЪҶЩҫ ШұШ§ $O_1$ ЩҲ Щ…ШұЪ©ШІ ШҜШ§ЫҢШұЩҮЩ” ШіЩ…ШӘ ШұШ§ШіШӘ ШұШ§ $O_2$ ШЁЩҶШ§Щ…ЫҢШҜ.
ЩҶЪ©ШӘЩҮвҖҢШ§ЫҢ Ъ©ЩҮ ШЁШұШ§ЫҢ Ш§ЫҢЩҶ ЩҫШұШіШҙ Щ…ШҜЩ‘ЩҶШёШұ ШЁЩҲШҜЩҮвҖҢШ§ШіШӘ Ш§ЫҢЩҶ Ш§ШіШӘ Ъ©ЩҮ Ъ©ЩҲШӘШ§ЩҮШӘШұЫҢЩҶ Щ…ШіЫҢШұ ШҜШұ ЩҮЩҶШҜШіЩҮЩ” Ш§ЩӮЩ„ЫҢШҜШіЫҢ ШЁЫҢЩҶ ЫҢЪ© ЩҶЩӮШ·ЩҮ ШӘШ§ Щ…ШұШІ ЫҢЪ© ШҜШ§ЫҢШұЩҮШҢ ЩҫШ§ШұЩҮвҖҢШ®Ш·ЫҢ Ш§ШіШӘ Ъ©ЩҮ ШЁШұ Щ…ШӯЫҢШ· ШҜШ§ЫҢШұЩҮ Ш№Щ…ЩҲШҜ ШЁШ§ШҙШҜ Ъ©ЩҮ ЩҮЩ…вҖҢШ§ШұШІ ШЁШ§ Ш§ЫҢЩҶ Ш§ШіШӘ Ъ©ЩҮ Ш§Щ…ШӘШҜШ§ШҜ ШҙШ№Ш§Ш№ЫҢ Ш§ШІ ШҜШ§ЫҢШұЩҮ ШЁШ§ШҙШҜ Ъ©ЩҮ ШЁШұ ШұЩҲЫҢ Ш®Ш· ЩҲШ§ШөЩ„ Щ…ШұЪ©ШІ ШҜШ§ЫҢШұЩҮ ЩҲ ШўЩҶ ЩҶЩӮШ·ЩҮ ЩӮШұШ§Шұ ШҜШ§ШұШҜ.
ЪҶЩҲЩҶ Щ…ЫҢвҖҢШ®ЩҲШ§ЩҮЫҢЩ… Щ…ШіШ§ЩҒШӘЫҢ ШұШ§ Ъ©ЩҮ ШІЫҢШұ ШіШ§ЫҢЩҮвҖҢШЁШ§ЩҶвҖҢЩҮШ§ ЫҢШ§ ЩҮЩ…Ш§ЩҶ ЪҶШ§ШҜШұЩҮШ§ ЩҶЫҢШіШӘЫҢЩ… ШұШ§ Ъ©Щ…ЫҢЩҶЩҮ Ъ©ЩҶЫҢЩ… ЩҫШі ШЁШ§ЫҢШҜ Ъ©Щ…ШӘШұЫҢЩҶ Щ…ШіШ§ЩҒШӘ ШұШ§ Ш§ШІ ЩҶЩӮШ·ЩҮЩ” $A$ ШӘШ§ ШҜШ§ЫҢШұЩҮЩ” ЪҶЩҫ ЩҲ ШіЩҫШі Ъ©Щ…ШӘШұЫҢЩҶ Щ…ШіШ§ЩҒШӘ ШұШ§ Ш§ШІ ШҜШ§ЫҢШұЩҮЩ” ЪҶЩҫ ШЁЩҮ ШҜШ§ЫҢШұЩҮЩ” ШұШ§ШіШӘ ЩҲ ШіЩҫШі Ъ©Щ…ШӘШұЫҢЩҶ Щ…ШіШ§ЩҒШӘ Ш§ШІ ШҜШ§ЫҢШұЩҮЩ” ШұШ§ШіШӘ ШӘШ§ ЩҶЩӮШ·ЩҮЩ” $B$ ШұШ§ ШЁШұЪҜШІЫҢЩҶЫҢЩ….
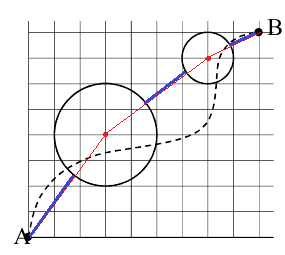
ШЁШ§ ШӘЩҲШ¬ЩҮ ШЁЩҮ ЩҶЪ©ШӘЩҮШҢ Ъ©ЩҲШӘШ§ЩҮШӘШұЫҢЩҶ Щ…ШіШ§ЩҒШӘ ШЁЫҢЩҶ $A$ ЩҲ ШҜШ§ЫҢШұЩҮЩ” ЪҶЩҫ ЩҫШ§ШұЩҮвҖҢШ®Ш·ЫҢ Ш§ШіШӘ Ъ©ЩҮ ШҜШұ ШӘШөЩҲЫҢШұ ЩҫШ§ШҰЫҢЩҶ ШЁШ§ ШұЩҶЪҜ ШўШЁЫҢ Ъ©ШҙЫҢШҜЩҮвҖҢШ§ЫҢЩ… Ъ©ЩҮ ШЁШұ ШұЩҲЫҢ ЩҫШ§ШұЩҮвҖҢШ®Ш· $AO_1$ ЩҶШҙШ§ЩҶ ШҜШ§ШҜЩҮвҖҢШ§ЫҢЩ…. Ъ©Щ„ $AO_1$ ШЁШ§ Ъ©Щ…Ъ© ЩӮШ§ЩҶЩҲЩҶ ШЁШ§ШЁЩ„ЫҢШ§ЩҶ (ЩҒЫҢШ«Ш§ШәЩҲШұШ«) ШЁШұШ§ШЁШұ Ш§ШіШӘ ШЁШ§ $\sqrt{3^2+4^2}$ ЩӮШіЩ…ШӘЫҢ Ш§ШІ Ш§ЫҢЩҶ ЩҫШ§ШұЩҮвҖҢШ®Ш· Ъ©ЩҮ ШҜШұЩҲЩҶ ШҜШ§ЫҢШұЩҮ ЩӮШұШ§Шұ ШҜШ§ШұШҜ ШҜЩӮЫҢЩӮШ§ЩӢ ЫҢЪ© ШҙШ№Ш§Ш№ Ш§ШІ Ш§ЫҢЩҶ ШҜШ§ЫҢШұЩҮ Ш§ШіШӘ ЩҫШі Щ…ШіШ§ЩҒШӘ Ш®Ш§ШұШ¬ Ш§ШІ ШўЩҶ ШЁШұШ§ШЁШұ Ш§ШіШӘ ШЁШ§ $5-2=3$. Ш§Ъ©ЩҶЩҲЩҶ ЩӮШіЩ…ШӘ ШўШЁЫҢвҖҢШұЩҶЪҜ ШҜЩҲЩ…. Ш§ЫҢЩҶ ЩҫШ§ШұЩҮвҖҢШ®Ш· ШЁШұШ§ШЁШұ ШЁШ§ ЩҫШ§ШұЩҮвҖҢШ®Ш· $O_1O_2$ Щ…ЩҶЩҮШ§ЫҢ ШҜЩҲ ШҙШ№Ш§Ш№ШҢ ЫҢЪ©ЫҢ Ш§ШІ ШҜШ§ЫҢШұЩҮЩ” ЪҶЩҫ ЩҲ ЫҢЪ©ЫҢ Ш§ШІ ШҜШ§ЫҢШұЩҮЩ” ШұШ§ШіШӘ. ЩҫШі ШҜШ§ШұШ§ШІШ§ЫҢ Ш§ЫҢЩҶ Щ…ШіШ§ЩҒШӘ ШЁШұШ§ШЁШұ Ш§ШіШӘ ШЁШ§
$\sqrt{(7-3)^2+(7-4)^2}-2-1=2$
ЩҲ Ш§Щ…Ш§ ЩӮШіЩ…ШӘ ЩҫШ§ЫҢШ§ЩҶЫҢ Ъ©ЩҮ ШЁШұШ§ШЁШұ Ш§ШіШӘ ШЁШ§ $O_2B$ Щ…ЩҶЩҮШ§ЫҢ ЫҢЪ© ШҙШ№Ш§Ш№ Ш§ШІ ШҜШ§ЫҢШұЩҮЩ” ШұШ§ШіШӘ. ЫҢШ№ЩҶЫҢ $\sqrt{(9-7)^2+(8-7)^2}-1=\sqrt{5}-1$.
ЩҫШі ШҜШұ Ъ©Щ„ Ш¬Щ…Ш№ ШҜШұШ§ШІШ§ЫҢ ШіЩҮ Щ…ШіШ§ЩҒШӘ ШўШЁЫҢ Ъ©ЩҮ ШЁШұШ§ШЁШұ Ъ©Щ…ШӘШұЫҢЩҶ Щ…ШіШ§ЩҒШӘ Щ…Щ…Ъ©ЩҶ ШІЫҢШұ ШЁШ§ШұШ§ЩҶ Ш§ШіШӘ Щ…ЫҢвҖҢШҙЩҲШҜШӣ
$3+2+\sqrt{5}-1=4+\sqrt{5}$.
ЪҜШІЫҢЩҶЩҮЩ” Ш§Щ„ЩҒ.