$n$توپ را در یک ردیف بچینید.
از سمت چپ به مقدار $x_1$توپ جدا کرده و یک خط قرار دهید دوباره $x_2$ توپ جداکرده و خطی می گذاریم و این کار را ادامه می دهیم.در واقع شکل زیر به دست می اید.
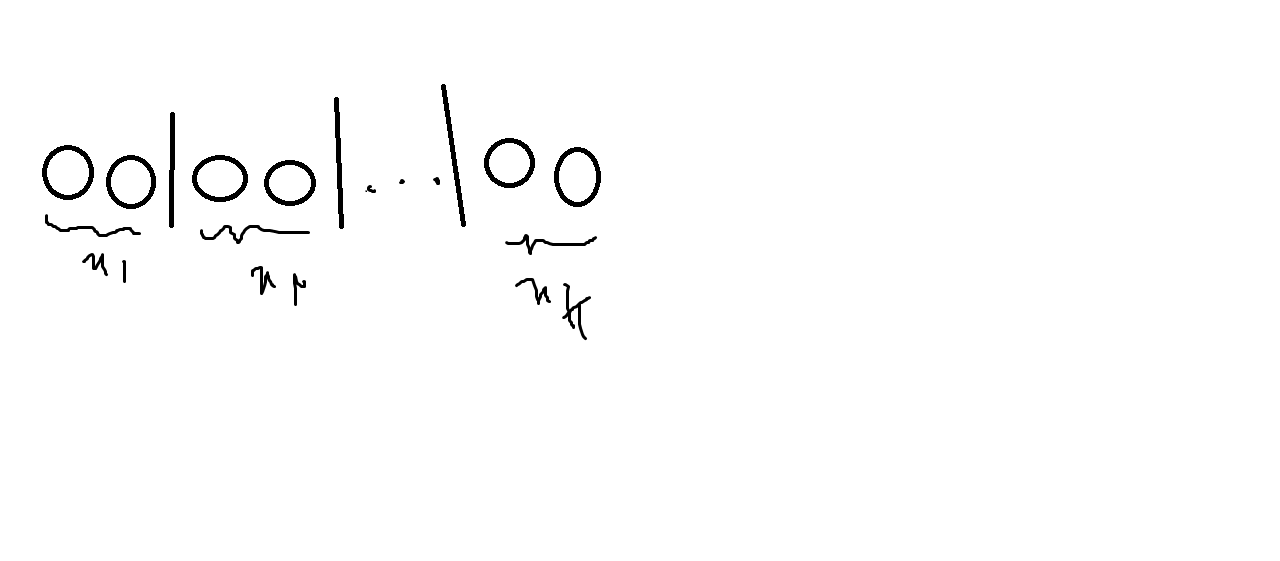
تعداد خط ها $k-1$ تا می باشد حال کافی است جایگشت های بین توپ و خط ها را حساب کنیم که برابر است با انتخاب $n$ شی از بین $n+k-1$ شی که برابر است با جواب مطلوب مسعله.