اگر متن درس را بخوانید و همینگونه با مدول کسرها آشنا باشید، پاسخ دادن به این تمرین آسان میشود.
مدول کسرها را اگر آشنایی ندارید در اینجا یادآور میشویم. اگر $R$ یک حلقه، $S$ یک زیرمجموعهٔ ضربی از آن و $M$ یک $R$-مدول باشد آنگاه مدول کسرهای $S^{-1}M$ را به مجموعهٔ
$$\{\dfrac{m}{s}|m\in M,s\in S\}$$
با عمل ضرب و جمع
$$\begin{array}{l}r\cdot\dfrac{m}{s}=\dfrac{rm}{s}\\
\dfrac{m_1}{s_1}+\dfrac{m_2}{s_2}=\dfrac{s_2m_1+s_1m_2}{s_1s_2}\end{array}$$
بعلاوهٔ اینکه
$$\dfrac{m_1}{s_1}=\dfrac{m_2}{s_2}\Longleftrightarrow\exists u\in S\text{ s.t. }u(s_2m_1-s_1m_2)=0$$
$R$
را یک دامنهٔ صحیح و
$M$
را یک
$R$
-مدول چپ بردارید. مجموعهٔ
$R-\{0\}$
یک زیرمجموعهٔ ضربی از
$R$
است، آن را
$S$
بنامید. توجه کنید که دامنهٔ صحیح بودن برای ثابت کردن مجموعهٔ ضربی بودن
$S$
نیاز میشود.
$K$
را میدان کسرهای
$R$
یعنی حلقهٔ کسرهای
$S^{-1}R$
قرار دهید. تعریف جهانی تانسور دو مدول را به یاد آورید. از آن تعریف استفاده و ثابت میکنیم که ضرب تانسوری
$K\otimes_R M$
برابر با
$S^{-1}M$
است. البته توجه کنید که نه تنها برای دامنههای صحیح و زیرمجموعهٔ ضربی خاصی که معرفی کردیم بلکه برای تمام حلقهها و زیرمجموعههای ضربیشان این حکم برقرار است. با توجه به تعریف نخست باید یک تابع دوخطی از
$K\times M$
به
$S^{-1}M$
تعریف کنیم. تابع
$f$
در زیر را درنظر بگیرید.
$$\left\{\begin{array}{rl}f:K\times M & \rightarrow S^{-1}M\\
(\dfrac{r}{s},m) & \mapsto r\dfrac{m}{s}\end{array}\right.$$
ثابت میکنیم که
$f$
دوخطی است.
$$\forall\dfrac{r_1}{s_1}\in K,\forall r\in R,\forall m_1,m_2\in M:$$
$$\begin{array}{rcl}
f(r\dfrac{r_1}{s_1}+\dfrac{r_2}{s_2},m_1) & = & f(\dfrac{rr_1s_2+r_2s_1}{s_1s_2},m_1)\\
& = & (rr_1s_2+r_2s_1)\dfrac{m_1}{s_1s_2}\\
& = & rr_1s2\dfrac{m_1}{s_1s_2}+r_2s_1\dfrac{m_1}{s_1s_2}\\
& = & rr_1\dfrac{m_1}{s_1}+r_2\dfrac{m_2}{s_2}\\
& = & rf(\dfrac{r_1}{s_1},m_1)+f(\dfrac{r_2}{s_2},m_1)
\end{array}$$
$$\begin{array}{rcl}
f(\dfrac{r_1}{s_1},rm_1+m_2) & = & r_1\dfrac{rm_1+m_2}{s_1}\\
& = & r_1r\dfrac{m_1}{s_1}+r_1\dfrac{m_2}{s_1}\\
& = & rf(\dfrac{r_1}{s_1},m_1)+f(\dfrac{r_1}{s_1},m_2)
\end{array}$$
اکنون باید ثابت کنید که اگر
$g:K\times M\rightarrow N$
یک تابع دوخطی دیگر از
$K\times M$
به یک
$R$
-مدول چپ دیگر باشد آنگاه یک
$R$
-همریختی مدولی یکتا از
$S^{-1}M$
به
$N$
وجود دارد که نمودار زیر را جابجایی میکند.
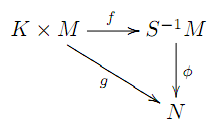
تعریف کنید
$$\left\{\begin{array}{rl}
\phi:S^{-1}M & \rightarrow N\\
\dfrac{m}{s} & \mapsto g(\dfrac{1}{s},m)
\end{array}\right.$$
در اینصورت
$$\forall\dfrac{m_1}{s_1},\dfrac{m_2}{s_2}\in S^{-1}M,\forall r\in R:$$
$$\begin{array}{rcl}
\phi(r\dfrac{m_1}{s_1}+\dfrac{m_2}{s_2}) & = & \phi(\dfrac{rs_2m_1+s_1m_2}{s_1s_2})\\
& = & g(\dfrac{1}{s_1s_2},rs_2m_1+s_1m_2)\\
& = & rs_2g(\dfrac{1}{s_1s_2},m_1)+s_1g(\dfrac{1}{s_1s_2},m_2)\\
& = & rg(\dfrac{s_2}{s_1s_2},m_1)+g(\dfrac{s_1}{s_1s_2},m_2)\\
& = & fg(\dfrac{1}{s_1},m_1)+g(\dfrac{1}{s_2},m_2)\\
& = & r\phi(\dfrac{m_1}{s_1})+\phi(\dfrac{m_2}{s_2})
\end{array}$$
پس
$\phi$
یک
$R$
-همریختی است. اینک فرض کنید
$\psi$
یک
$R$
-همریختی از
$S^{-1}M$
به
$N$
باشد که نمودار را جابجایی کند. باید ثابت کنیم که با
$\phi$
برابر است.
$$\begin{array}{rl}
\forall s\in S,m\in M\;:\;\psi(\dfrac{m}{s}) & =\psi(f(\dfrac{1}{s},m))\\
& =g(\dfrac{1}{s},m)\\
& =\phi(f(\dfrac{1}{s},m))\\
& =\phi(\dfrac{m}{s})
\end{array}$$
در نتیجه
$\psi=\phi$
. خودتان جزئیاتی همچون تابعبودنها و دوتایی بدون عملها را در لابهلای مراحل بالا تکمیل کنید و جاههایی که تساویها به خاطر دوخطی بودن تابعهای دوخطی روی دادهاند را دقت کنید، هیچ تساویای به خاطر اینکه قرار است برای حکم به از آن بگذریم دستی اضافه نشدهاست و حتما دلیلی قابل استناد داشتهاست که چرا این تساوی را میشدهاست نوشت. اگر از جزئیات بدون داشتن دلیل برقرار بودنشان بگذرید هیچ چیزی نمیآموزید.
و اما تا اینجا هنوز به پرسش اصلی حمله نکردهایم. پرسش اصلی میگوید ثابت کنید که اگر
$\phi$
،
$R$
-همریختی مدولی زیر باشد
$$\left\{\begin{array}{rl}
M & \rightarrow K\otimes_R M\\
M & \mapsto 1\otimes m
\end{array}\right.$$
ثابت کنید
$\ker\phi=tor(M)$
. که
$tor(M)=\{m\in M|\exists r\in R-\{0\}\text{ s.t }rm=0\}$
. اگر توجه کنید تعریف
$tor(M)$
به
$S^{-1}M$
باید ربط داشتهباشد! نخست بیاییم
$K\otimes_RM$
را که اکنون میدانیم چیست را در تعریف
$\phi$
تعویض کنیم.
$$\left\{\begin{array}{rl}
M & \rightarrow S^{-1}M\\
M & \mapsto \dfrac{m}{1}
\end{array}\right.$$
بفرض
$m\in tor(M)$
پس باید عنصر ناصفری از
$R$
و در نتیجه داخل
$S$
باشد که ضربش در
$m$
صفر شدهاست. آن را
$s$
بنامید.
$$\phi(m)=\dfrac{m}{1}=\dfrac{sm}{s1}=\dfrac{0}{s}=0$$
پس
$m\in\ker\phi$
. این بار فرض کنید
$m\in\ker\phi$
پس
$\dfrac{m}{1}=\phi(m)=0$
. اینکه
$\dfrac{m}{1}$
مساوی صفر شدهاست و
$0=\dfrac{0}{1}$
با توجه به تعریف مدول کسرها یعنی
$$\begin{array}{l}\exists s\in S\text{ s.t. }s(1.m-1.0)=0\\ \exists s\in S\text{ s.t }sm=0\end{array}$$
و چون
$S=R-\{0\}$
، این دقیقا یعنی
$m\in tor(M)$
.