ШЁШұШ§ЫҢ Ш§ЫҢЩҶЪ©ЩҮ ШЁЪҜЩҲШҰЫҢЩ… ШҙШұШ· ЫҢШ§ ЩҒШұШ¶ Ш§Щ„ЩҒ ШЁШұШ§ЫҢ ЩӮШ¶ЫҢЩҮ ЫҢШ§ ШӯЪ©Щ…ЫҢ Ъ©ЩҮ Ш«Ш§ШЁШӘ Ъ©ШұШҜЩҮвҖҢШ§ЫҢЩ… Щ„Ш§ШІЩ… Ш§ШіШӘ ШЁШ§ЫҢШҜ ЩҶЩ…ЩҲЩҶЩҮвҖҢШ§ЫҢ ШЁЫҢШ§ЩҲШұЫҢЩ… Ъ©ЩҮ Ш§ЫҢЩҶ ШҙШұШ· ШЁШұЩӮШұШ§Шұ ЩҶЫҢШіШӘ ЩҲ ШӯЪ©Щ… ШЁШұЩӮШұШ§Шұ ЩҶШҙШҜЩҮвҖҢШ§ШіШӘ ШҜШұ ШөЩҲШұШӘЫҢЪ©ЩҮ ЪҶЩҶЫҢЩҶ ЩҶЩ…ЩҲЩҶЩҮвҖҢШ§ЫҢ ЩҲШ¬ЩҲШҜ ЩҶШҜШ§ШҙШӘЩҮ ШЁШ§ШҙШҜ Ш§ЫҢЩҶ ЩҒЪ©Шұ ШЁЩҮ Ш°ЩҮЩҶ Щ…ЫҢвҖҢШўЫҢШҜ Ъ©ЩҮ Ш®ШЁ ЪҶШұШ§ ШЁШ§ЫҢШҜ ШҙШұШ· Ш§Щ„ЩҒ ШұШ§ ШҜШұ ШөЩҲШұШӘ ЩӮШ¶ЫҢЩҮ ШЁЪҜШ°Ш§ШұЫҢЩ… ШІЩ…Ш§ЩҶЫҢвҖҢЪ©ЩҮ ШЁШҜЩҲЩҶ ШўЩҶ ЩҶЫҢШІ ШӯЪ©Щ… ШЁШұЩӮШұШ§Шұ Ш§ШіШӘШҹ ШЁЩҶШ§ШЁШұШ§ЫҢЩҶ Ш§ЫҢЩҶ ЩҶЩҲШ№ ЩҫШұШіШҙ ЫҢЪ©ЫҢ Ш§ШІ ЩҫШұШіШҙвҖҢЩҮШ§ЫҢ ШұШ§ЫҢШ¬ЫҢ ЩҮШіШӘЩҶШҜ Ъ©ЩҮ ШҜШұ ЩҮЩҶЪҜШ§Щ… ШұЩҲЫҢШ§ШұЩҲЫҢЫҢ ШЁШ§ ЫҢЪ© ЩӮШ¶ЫҢЩҮЩ” Ш¬ШҜЫҢШҜ ШЁШ§ЫҢШҜ Ш§ШІ Ш®ЩҲШҜШӘШ§ЩҶ ШЁЩҫШұШіЫҢШҜ. ШЁШұШ®ЫҢ ЩӮШ¶ЫҢЩҮвҖҢЩҮШ§ЫҢ Ш¬ШҜЫҢШҜ Ъ©ЩҮ ШӘЩҲШіЫҢШ№ ЩҲ ШӘШ№Щ…ЫҢЩ… ЩӮШ¶ЫҢЩҮвҖҢЩҮШ§ЫҢ ШҜЫҢЪҜШұЫҢ ЩҮШіШӘЩҶШҜ ШӯШ§ШөЩ„ ЩҫШұШіЫҢШҜЩҶ Ш§ЫҢЩҶвҖҢЪҜЩҲЩҶЩҮ ЩҫШұШіШҙвҖҢЩҮШ§ ШЁЩҲШҜЩҮвҖҢШ§ЩҶШҜ. ЫҢШ№ЩҶЫҢ ЩҮЫҢЪҶ ЩҶЩ…ЩҲЩҶЩҮвҖҢШ§ЫҢ ЩҶЫҢШ§ЩҒШӘЩҶШҜ Ъ©ЩҮ Щ„Ш§ШІЩ… ШЁЩҲШҜЩҶ ШҙШұШ· ШұШ§ ЩҶШҙШ§ЩҶ ШҜЩҮШҜ ЩҲ ШіЩҫШі ШЁЩҮ ШҜЩҶШЁШ§Щ„ Ш§Ш«ШЁШ§ШӘ ЩӮШ¶ЫҢЩҮ ШҜШұ ШӯШ§Щ„ШӘ Ъ©Щ„ЫҢвҖҢШӘШұ ШЁШҜЩҲЩҶ ЩҒШұШ¶ Ъ©ШұШҜЩҶ Ш§ЫҢЩҶ ШҙШұШ· Ш§Ш¶Ш§ЩҒЩҮ ШұЩҒШӘЩҮвҖҢШ§ЩҶШҜ.
ШЁЩҮ ЩҮШұ ШӯШ§Щ„ ШЁШұШ§ЫҢ Ш§ЫҢЩҶ ЩҫШұШіШҙ ШҜЩҲ ЩҒШұШ¶ ЩҮШіШӘ ЩҲ Ъ©Ш§ШұЫҢ Ъ©ЩҮ ШЁШ§ЫҢШҜ ШЁЪ©ЩҶЫҢЩ… Ш§ЫҢЩҶ Ш§ШіШӘ Ъ©ЩҮ ШЁШұШ§ЫҢ ЩҮШұ ЫҢЪ© Ш§ШІ Ш§ЫҢЩҶ ЩҒШұШ¶вҖҢЩҮШ§ ШҜШіШӘвҖҢЪ©Щ… ЫҢЪ© ЩҶЩ…ЩҲЩҶЩҮ ШЁЫҢШ§ЩҲШұЫҢЩ… Ъ©ЩҮ Щ„Ш§ШІЩ… ШЁЩҲШҜЩҶШҙ ШұШ§ ЩҶШҙШ§ЩҶ ШҜЩҮШҜ. ЩҮШұ ШҜЩҲ ЩҶЩ…ЩҲЩҶЩҮвҖҢШ§ЫҢ Ъ©ЩҮ ШҜШұ Ш§ЫҢЩҶШ¬Ш§ Щ…ЫҢвҖҢШ®ЩҲШ§ЩҮЫҢЩ… ШЁЫҢШ§ЩҲШұЫҢЩ… ЩҶЩ…ЩҲЩҶЩҮвҖҢЩҮШ§ЫҢ Щ…ШҙЩҮЩҲШұЫҢ ЩҮШіШӘЩҶШҜ ШЁЩҮ Ш§ЫҢЩҶ Щ…Ш№ЩҶШ§ Ъ©ЩҮ ШӘЩӮШұЫҢШЁШ§ ШӘЩ…Ш§Щ… Ш§ЩҒШұШ§ШҜЫҢ Ъ©ЩҮ ШЁШ§ Ш§ЫҢЩҶ Щ…ЩҲШ¶ЩҲШ№вҖҢЩҮШ§ ШіШұ ЩҲ Ъ©Ш§Шұ ШҜШ§ШұЩҶШҜ ШўЩҶвҖҢШұШ§ ШҙЩҶЫҢШҜЩҮвҖҢШ§ЩҶШҜ.
ЩҫЫҢШҙ Ш§ШІ Ш§ЫҢЩҶЪ©ЩҮ Ш§ШҜШ§Щ…ЩҮ ШҜЩҮЫҢЩ… Ш§ШҙШ§ШұЩҮ Щ…ЫҢвҖҢЪ©ЩҶЫҢЩ… Ъ©ЩҮ ЫҢЪ© ЪҜШұЩҲЩҮ
$G$
ШұЩҲЫҢ ЫҢЪ© Щ…ЫҢШҜШ§ЩҶ
$F$
ЩҶЩ…Ш§ЫҢШҙ ШЁЩҮ Ш·ЩҲШұ Ъ©Ш§Щ…Щ„ Ъ©Ш§ЩҮШҙвҖҢЩҫШ°ЫҢШұ ШҜШ§ШұШҜ Ш§ЪҜШұ
$FG$
Щ…ШҜЩҲЩ„ Щ…ШӘЩҶШ§ШёШұ ШЁЩҮ Ш§ЫҢЩҶ ЩҶЩ…Ш§ЫҢШҙ ШЁЩҮ Ш·ЩҲШұ Ъ©Ш§Щ…Щ„ Ъ©Ш§ЩҮШҙвҖҢЩҫШ°ЫҢШұ ШЁШ§ШҙШҜ. ЫҢЪ© Щ…ШҜЩҲЩ„ ЩҶЫҢШІ ШЁЩҮ Ш·ЩҲШұ Ъ©Ш§Щ…Щ„ Ъ©Ш§ЩҮШҙвҖҢЩҫШ°ЫҢШұ Ш§ШіШӘ ЩҮШұ ЪҜШ§ЩҮ ШЁШӘЩҲШ§ЩҶ ШўЩҶвҖҢШұШ§ ШЁЩҮ ШҙЪ©Щ„ Ш¬Щ…Ш№ Щ…ШіШӘЩӮЫҢЩ…ЫҢ Ш§ШІ ШІЫҢШұЩ…ШҜЩҲЩ„вҖҢЩҮШ§ЫҢШҙ ЩҶЩҲШҙШӘ.
ШЁШұШ§ЫҢ ШЁШ®Шҙ ЩҶШ®ШіШӘШҢ ЫҢШ№ЩҶЫҢ Щ„Ш§ШІЩ… ШЁЩҲШҜЩҶ ШҙШұШ· ЩҶШҙЩ…ШұШҜЩҮвҖҢШҙШҜЩҶ Щ…ШұШӘШЁЩҮЩ” ЪҜШұЩҲЩҮ ШЁЩҲШіЫҢЩ„ЩҮЩ” Щ…ШҙШ®ШөЩҮЩ” Щ…ЫҢШҜШ§ЩҶ Ш§ШІ ШӘШ№ШұЫҢЩҒ ШЁЩҮвҖҢШ·ЩҲШұ Ъ©Ш§Щ…Щ„ Ъ©Ш§ЩҮШҙвҖҢЩҫШ°ЫҢШұ ШЁЩҲШҜЩҶ Ш§ШіШӘЩҒШ§ШҜЩҮ Щ…ЫҢвҖҢЪ©ЩҶЫҢЩ….
ШұШ§ШӯШӘвҖҢШӘШұЫҢЩҶ ШӯШ§Щ„ШӘ Ш§ЫҢЩҶ Ш§ШіШӘ Ъ©ЩҮ ЩҮШұ ШҜЩҲЫҢ ЪҜШұЩҲЩҮ ЩҲ Щ…ЫҢШҜШ§ЩҶ ШұШ§
$\mathbb{Z}_2$
ШЁШұШҜШ§ШұЫҢЩ…. Ш§ЫҢЩҶ Щ…Ш¬Щ…ЩҲШ№ЩҮ ШЁЩҮ ЩҮЩ…ШұШ§ЩҮ Ш¬Щ…Ш№ ЩҲ Ш¶ШұШЁ ШұШҜЩҮвҖҢЩҮШ§ЫҢ ШЁШ§ЩӮЫҢЩ…Ш§ЩҶШҜЩҮвҖҢШ§ЫҢ ШЁЩҮ ЩҫЫҢЩ…Ш§ЩҶЩҮЩ” ЫІ ШӘШҙЪ©ЫҢЩ„ ЩҮЩ… ЪҜШұЩҲЩҮ ЩҲ ЩҮЩ… Щ…ЫҢШҜШ§ЩҶ Щ…ЫҢвҖҢШҜЩҮШҜ. Щ…ШұШӘШЁЩҮ ЩҲ Щ…ШҙШ®ШөЩҮЩ” ШўЩҶ ЩҮШұ ШҜЩҲ ЫІ ЩҮШіШӘЩҶШҜ Ъ©ЩҮ ШўШҙЪ©Ш§ШұШ§ Ш№ШҜШҜ ШҜЩҲШҢ Ш№ШҜШҜ ШҜЩҲ ШұШ§ Щ…ЫҢвҖҢШҙЩ…Ш§ШұШҜ. ШЁШұШ§ЫҢ Ш§ЫҢЩҶЪ©ЩҮ Ш§Ш№Ш¶Ш§ЫҢ ЪҜШұЩҲЩҮ ЩҲ Щ…ЫҢШҜШ§ЩҶЩ…Ш§ЩҶ ШұШ§ ШЁШ§ ЩҮЩ… Ш§ШҙШӘШЁШ§ЩҮ ЩҶЪҜЫҢШұЫҢЩ…ШҢ Ш§Ш№Ш¶Ш§ЫҢ
$\mathbb{Z}_2$
ШұШ§ ШІЩ…Ш§ЩҶЫҢвҖҢЪ©ЩҮ ШЁЩҮ ЪҶШҙЩ… ЪҜШұЩҲЩҮ Щ…ЫҢвҖҢШЁЫҢЩҶЫҢЩ… ШЁШ§
$e,a$
ЩҶЩ…Ш§ЫҢШҙ Щ…ЫҢвҖҢШҜЩҮЫҢЩ… ЩҲ ШІЩ…Ш§ЩҶЫҢвҖҢЪ©ЩҮ ШЁЩҮ ЪҶШҙЩ… Щ…ЫҢШҜШ§ЩҶ Щ…ЫҢвҖҢШЁЫҢЩҶЫҢЩ… ШЁШ§ Ы° ЩҲ Ыұ ЩҶЩ…Ш§ЫҢШҙ Щ…ЫҢвҖҢШҜЩҮЫҢЩ…. ЩҶШ®ШіШӘЫҢЩҶ Ъ©Ш§ШұЫҢ Ъ©ЩҮ ШЁШ§ЫҢШҜ ШЁЪ©ЩҶЫҢЩ… Ш§ЫҢЩҶ Ш§ШіШӘ Ъ©ЩҮ ШӯЩ„ЩӮЩҮЩ”
$FG$
ШұШ§ ШӘШҙЪ©ЫҢЩ„ ШЁШҜЩҮЫҢЩ…. Ш§ЫҢЩҶ ШӯЩ„ЩӮЩҮ ЫҢЪ© Щ…Ш¬Щ…ЩҲШ№ЩҮ Ш§ШІ Ш¬Щ…Ш№вҖҢЩҮШ§ЫҢ ЩҶЩ…Ш§ШҜЫҢЩҶ Ш§ШіШӘ ЫҢШ№ЩҶЫҢ
$$\{r_ee+r_aa|r_e,r_a\in \{0,1\}\}$$
ШӘЩҲШ¬ЩҮ Ъ©ЩҶЫҢШҜ Ъ©ЩҮ ШӯЩӮ ЩҶШҜШ§ШұЫҢЩ… ШЁЫҢШ§ЫҢЫҢЩ… ЩҲ Ы° ЩҲ Ыұ ШұШ§ ШЁШ§
$e,a$
Ш¶ШұШЁ Ъ©ЩҶЫҢЩ… ЩҲ ШіШ§ШҜЩҮ Ъ©ЩҶЫҢЩ… ШЁЩ„Ъ©ЩҮ ШҜЩӮЫҢЩӮШ§ ШЁЩҮ ШҙЪ©Щ„ ЩҶЩ…Ш§ШҜЫҢЩҶ ШІЫҢШұ Ш§Ш№Ш¶Ш§ ЩӮШұШ§Шұ Щ…ЫҢвҖҢЪҜЫҢШұЩҶШҜ ЩҲ ЩҮЫҢЪҶ ЪҜЩҲЩҶЩҮ ШіШ§ШҜЩҮвҖҢШіШ§ШІЫҢвҖҢШ§ЫҢ ШҜШұ Ъ©Ш§Шұ ЩҶЫҢШіШӘ
$$FG=\{0e+0a,1e+0a,0e+1a,1e+1a\}$$
ШЁШұШ®ЫҢ Ш§ШІ ЩӮШұШ§ШұШҜШ§ШҜ ЩҶЩ…Ш§ШҜЪҜШ°Ш§ШұЫҢ ШІЫҢШұ ШЁШұШ§ЫҢ Ъ©Щ…ШӘШұЩҶЩҲЫҢШіЫҢ ШҜШұ Ш§ЫҢЩҶ ЩҶЩ…ЩҲЩҶЩҮ Ъ©Щ…Ъ© Щ…ЫҢвҖҢЪҜЫҢШұЩҶШҜ ЩҲЩ„ЫҢ Ш§ЪҜШұ ШЁШұШ§ЫҢШӘШ§ЩҶ Ш§ШЁЩҮШ§Щ… Щ…ЫҢвҖҢШіШ§ШІШҜ ЩҲ ШӘШөЩҲШұ ШіШ§ШҜЩҮвҖҢШҙШҜЩҶ ШЁЩҮ Ш°ЩҮЩҶШӘШ§ЩҶ Щ…ЫҢвҖҢШўЫҢШҜ Ш§ШІ Ш§ЫҢЩҶ ШіШ§ШҜЩҮвҖҢШіШ§ШІЫҢ Ш§ШіШӘЩҒШ§ШҜЩҮ ЩҶЪ©ЩҶЫҢШҜ ЩҲ Ш§Ш№Ш¶Ш§ЫҢ
$FG$
ШұШ§ Ъ©Ш§Щ…Щ„ ШЁЩҶЩҲЫҢШіЫҢШҜ.
$$0:=0e+0a,e:=1e+0a,a:=0e+1a,a+e:=1e+1a$$
ЩҮШұ
$FG$
Щ…ШҜЩҲЩ„ Щ…ШӘЩҶШ§ШёШұ ШЁЩҮ ЫҢЪ©
$F$
ЩҶЩ…Ш§ЫҢШҙ Ш§ШІ
$G$
Ш§ШіШӘ ЩҲ ШӯЪ©Щ… ЩӮШ¶ЫҢЩҮ Щ…ЫҢвҖҢЪҜЩҒШӘ Ъ©ЩҮ ЩҮШұ
$F$
ЩҶЩ…Ш§ЫҢШҙШҢ ШЁЩҮ Ш·ЩҲШұ Ъ©Ш§Щ…Щ„ Ъ©Ш§ЩҮШҙвҖҢЩҫШ°ЫҢШұ Ш§ШіШӘ ЩҫШі Ш§ЪҜШұ ЫҢЪ©
$F$
ЩҶЩ…Ш§ЫҢШҙ Ъ©ЩҮ ШЁЩҮ Ш·ЩҲШұ Ъ©Ш§Щ…Щ„ Ъ©Ш§ЩҮШҙвҖҢЩҫШ°ЫҢШұ ЩҶШЁШ§ШҙШҜ ЩҶЫҢШІ ШЁЫҢШ§ШЁЫҢЩ… Ъ©Ш§Шұ ШӘЩ…Ш§Щ… Ш§ШіШӘ. ШҜШұ ЩҲШ§ЩӮШ№ ЩҮЩ…вҖҢШ§ШұШІ ШЁШ§ Ш§ЫҢЩҶ Щ…ЫҢвҖҢШҙЩҲШҜ Ъ©ЩҮ ЫҢЪ©
$FG$
Щ…ШҜЩҲЩ„ ШЁЫҢШ§ШЁЫҢЩ… Ъ©ЩҮ Ш¬Щ…Ш№вҖҢЩ…ШіШӘЩӮЫҢЩ… ШІЫҢШұЩ…ШҜЩҲЩ„вҖҢЩҮШ§ЫҢШҙ ЩҶШҙЩҲШҜ. ШіШ§ШҜЩҮвҖҢШӘШұЫҢЩҶ
$R$
Щ…ШҜЩҲЩ„ ШЁШұШ§ЫҢ ЫҢЪ© ШӯЩ„ЩӮЩҮ ШҜЩ„Ш®ЩҲШ§ЩҮШҢ Ш®ЩҲШҜШҙ Ш§ШіШӘ. ЩҫШі ШЁЫҢШ§ЫҢЫҢЩ… Ш§ШІ Ш®ЩҲШҜ
$FG$
ШЁЩҮ Ш№ЩҶЩҲШ§ЩҶ
$FG$
Щ…ШҜЩҲЩ„ ШҙШұЩҲШ№ ШЁЩҮ ШЁШұШұШіЫҢ Ъ©ЩҶЫҢЩ…. ЫҢЪ© ШӯЩ„ЩӮЩҮ ШЁЩҮ Ш№ЩҶЩҲШ§ЩҶ Щ…ШҜЩҲЩ„ ШұЩҲЫҢ Ш®ЩҲШҜШҙ ШЁШ§ Ш¬Щ…Ш№ ШӯЩ„ЩӮЩҮвҖҢШ§ЫҢ ЩҲ Ш¶ШұШЁ ШӯЩ„ЩӮЩҮвҖҢШ§ЫҢвҖҢШ§Шҙ ШЁЩҮ Ш№ЩҶЩҲШ§ЩҶ Ш¬Щ…Ш№ Щ…ШҜЩҲЩ„ЫҢ ЩҲ Ш¶ШұШЁ Ш§ШіЪ©Ш§Щ„ШұЫҢ Щ…ШҜЩҲЩ„ЫҢ ШҜШұ ЩҶШёШұ ЪҜШұЩҒШӘЩҮ Щ…ЫҢвҖҢШҙЩҲШҜ (Ш§Щ„ШЁШӘЩҮ ШЁШұШ§ЫҢ ШЁШұШ®ЫҢ ШӯЩ„ЩӮЩҮвҖҢЩҮШ§ ШіШ§Ш®ШӘШ§ШұЩҮШ§ЫҢ ШЁЫҢШҙШӘШұЫҢ ШЁШ§ ШҜШұ ЩҶШёШұ ЪҜШұЩҒШӘЩҶ Ш¬Щ…Ш№ ЩҲ Ш¶ШұШЁ Щ…ШӘЩҒШ§ЩҲШӘ Щ…ЫҢвҖҢШӘЩҲШ§ЩҶ ШіШ§Ш®ШӘ ЩҲЩ„ЫҢ Щ…Ш§ ШҜШұ Ш§ЫҢЩҶШ¬Ш§ ШЁШ§ Ш®ЩҲШҜ ШіШ§Ш®ШӘШ§Шұ ШЁШҜЫҢЩҮЫҢ ЩҶЫҢШІ Ъ©Ш§Шұ ШұШ§ ШЁЩҮ Ш§ЩҶШ¬Ш§Щ… Ш®ЩҲШ§ЩҮЫҢЩ… ШұШіШ§ЩҶШҜ). ЪҶЩҲЩҶ ЪҶЩҮШ§Шұ Ш№ЩҶШөШұ ШЁЫҢШҙШӘШұ ЩҶШҜШ§ШұШҜ ШЁЪҜШ°Ш§ШұЫҢШҜ Ш¬ШҜЩҲЩ„ Ш§Ш№Щ…Ш§Щ„Шҙ ШұШ§ Ъ©Ш§Щ…Щ„ ШЁЫҢШ§ЩҲШұЫҢЩ….
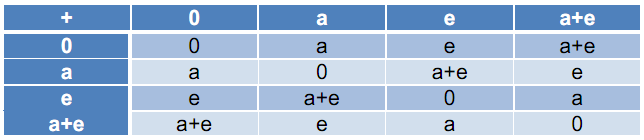

ШӯЩҲШ§ШіШӘШ§ЩҶ ШЁШ§ШҙШҜ Ъ©ЩҮ Щ…ЩҶШёЩҲШұ Ш§ШІ ЩҶЩ…Ш§ШҜЩҮШ§ЫҢ ШҜШ§Ш®Щ„ Ш¬ШҜЩҲЩ„ ЪҶЩҮ Ш§ШіШӘ ЩҲ Ш¬Щ…Ш№ ЩҲ Ш¶ШұШЁ
$FG$
ЪҶЪҜЩҲЩҶЩҮ ШӘШ№ШұЫҢЩҒ Щ…ЫҢвҖҢШҙЩҲШҜ ЩҲ ШЁШ§ШІ ШӘЪ©ШұШ§Шұ Щ…ЫҢвҖҢЪ©ЩҶЩ… Ъ©ЩҮ ШіШ§ШҜЩҮвҖҢШіШ§ШІЫҢвҖҢЩҮШ§ЫҢ Ш§Ш¶Ш§ЩҒЫҢ ЩҲ ЩҶШ§ШҜШұШіШӘ Ш§ЩҶШ¬Ш§Щ… ЩҶШҜЩҮЫҢШҜ. ШЁШұШ§ЫҢ Ш§ЫҢЩҶЪ©ЩҮ ШЁШЁЫҢЩҶЫҢШҜ ЪҶЪҜЩҲЩҶЩҮ Ш§ЫҢЩҶ Ш¬Щ…Ш№ ЩҲ Ш¶ШұШЁвҖҢЩҮШ§ ШөЩҲШұШӘ ЪҜШұЩҒШӘЩҮвҖҢШ§ЩҶШҜ Ш§ШІ Ш¬Щ…Ш№ ЩҲ Ш¶ШұШЁ ЩҮШұ Ъ©ШҜШ§Щ… ЫҢЪ© ЩҶЩ…ЩҲЩҶЩҮ ШҜШұ ШІЫҢШұ Щ…ЫҢвҖҢШўЩҲШұЫҢЩ…. ШЁШ№Щ„Ш§ЩҲЩҮ ШӯЩҲШ§ШіШӘШ§ЩҶ ШЁШ§ШҙШҜ Ъ©ЩҮ Ш№Щ…Щ„ ЪҜШұЩҲЩҮ
$\mathbb{Z}_2$
ШұШ§ Ш№Щ…Щ„ Ш¬Щ…Ш№ ЪҜШұЩҒШӘЩҮвҖҢШ§ЫҢЩ… ШЁЩҶШ§ШЁШұШ§ЫҢЩҶ ШЁШ§ Ш§ЫҢЩҶЪ©ЩҮ Щ…Щ…Ъ©ЩҶ Ш§ШіШӘ ШЁШұШ®ЫҢвҖҢШӘШ§ЩҶ ЩҒЪ©Шұ Ъ©ЩҶЫҢШҜ
aa
ШЁШ§ЫҢШҜ Ш¶ШұШЁ ШұШҜЩҮЩ” ЫҢЪ© ШҜШұ ШұШҜЩҮЩ” ЫҢЪ© ЩҲ ШЁЩҶШ§ШЁШұШ§ЫҢЩҶ ШӯШ§ШөЩ„ ШұШҜЩҮЩ” ЫҢЪ© ШҙЩҲШҜШҢ Ш§ЫҢЩҶ ШЁЩҮ Щ…Ш№ЩҶШ§ЫҢ Ш¬Щ…Ш№ ШұШҜЩҮЩ” ЫҢЪ© ШЁШ§ ШұШҜЩҮЩ” ЫҢЪ© ЩҲ ШҜШұ ЩҶШӘЫҢШ¬ЩҮ ШӯШ§ШөЩ„ ШұШҜЩҮЩ” ШөЩҒШұ Щ…ЫҢвҖҢШҙЩҲШҜ ЫҢШ№ЩҶЫҢ
e.
$$\begin{array}{l}0+e=(0e+0a)+(1e+0a)=(0+1)e+(0+0)a=1e+0a=e\\aГ—a=(0e+1a)(0e+1a)=00ee+01ea+10ae+11aa=0e+0a+0a+1e=1e+0a=e\end{array} $$
Ш§ЪҜШұ ШӘЩҲШ¬ЩҮ Ъ©ЩҶЫҢШҜ ШӘЩҶЩҮШ§ ШІЫҢШұЩ…ШҜЩҲЩ„ (Ш§ЫҢШҜЩҮвҖҢШўЩ„) ЩҶШ§ШЁШҜЫҢЩҮЫҢ
$FG$
ШЁШұШ§ШЁШұ ШЁШ§ ШІЫҢШұЩ…ШҜЩҲЩ„ ШӘЩҲЩ„ЫҢШҜ ШҙШҜЩҮ ШЁЩҲШіЫҢЩ„ЩҮЩ”
$a+e$
Ш§ШіШӘ Ъ©ЩҮ ШҜЩҲ Ш№Ш¶ЩҲЫҢ
$\{0,a+e\}$
Щ…ЫҢвҖҢШҙЩҲШҜ. Ш§ЫҢЩҶ ШӘЩҶЩҮШ§ ШІЫҢШұЩ…ШҜЩҲЩ„ ЩҶШ§ШЁШҜЫҢЩҮЫҢ Ш§ШіШӘ Ъ©ЩҮ Ш¬Щ…Ш№Шҙ ШЁШ§ Ш®ЩҲШҜШҙ Ш®ЩҲШҜШҙ Щ…ЫҢвҖҢШҙЩҲШҜ. Ш§Щ„ШЁШӘЩҮ ШҜШұ Ш¬Щ…Ш№ Щ…ШіШӘЩӮЫҢЩ… Ш§ШҙШӘШұШ§Ъ© ШІЫҢШұЩ…ШҜЩҲЩ„вҖҢЩҮШ§ ШЁШ§ЫҢШҜ ШӘЪ©вҖҢШ№Ш¶ЩҲЫҢ ШөЩҒШұ ШЁШ§ШҙШҜ ЩҫШі ШӯШӘЫҢ ШЁЩҮ Ш§ЫҢЩҶЪ©ЩҮ Ш¬Щ…Ш№Шҙ ШЁШ§ Ш®ЩҲШҜШҙШҢ Ъ©Щ„
$FG$
ЩҶЩ…ЫҢвҖҢШҙЩҲШҜ ЩҶЫҢШІ ЩҶЫҢШ§ШІ ЩҶЫҢШіШӘ Ш§ШҙШ§ШұЩҮ Ъ©ЩҶЫҢЩ…. ШҜШұ ЩҶШӘЫҢШ¬ЩҮ ШЁЩҮ ЩҮЫҢЪҶ ЩҲШ¬ЩҮ ЩҶЩ…ЫҢвҖҢШҙЩҲШҜ Ш§ЫҢЩҶ Щ…ШҜЩҲЩ„ ШұШ§ ШЁЩҮ ШҙЪ©Щ„ Ш¬Щ…Ш№ Щ…ШіШӘЩӮЫҢЩ…ЫҢ Ш§ШІ ШІЫҢШұЩ…ШҜЩҲЩ„вҖҢЩҮШ§ЫҢШҙ ЩҶЩҲШҙШӘ ЩҲ Ш§ЫҢЩҶ Ш§Ш«ШЁШ§ШӘ ШұШ§ ШӘЩ…Ш§Щ… Щ…ЫҢвҖҢЪ©ЩҶШҜ.
Ш§Ъ©ЩҶЩҲЩҶ ШЁЩҮ ШіШұШ§Шә ШҙШұШ· ШҜЩҲЩ… ЩӮШ¶ЫҢЩҮ ЫҢШ№ЩҶЫҢ Щ…ШӘЩҶШ§ЩҮЫҢ ШЁЩҲШҜЩҶ ЪҜШұЩҲЩҮЩ…Ш§ЩҶ ШЁШұЩҲЫҢЩ…. ШіШ§ШҜЩҮвҖҢШӘШұЫҢЩҶ ЪҜШұЩҲЩҮ ЩҶШ§Щ…ШӘЩҶШ§ЩҮЫҢ Ъ©ЩҮ ШЁЩҮ Ш°ЩҮЩҶ Щ…ЫҢвҖҢШұШіШҜ Ш§Ш№ШҜШ§ШҜ ШөШӯЫҢШӯ ШЁШ§ Ш№Щ…Щ„ Ш¬Щ…Ш№ Ш§ШіШӘ. Щ…ЫҢШҜШ§ЩҶ ШұШ§ ЩҶЫҢШІ Щ…ЫҢШҜШ§ЩҶ Ш§Ш№ШҜШ§ШҜ Щ…Ш®ШӘЩ„Ш· (ЫҢШ§ ШӯЩӮЫҢЩӮЫҢ ЫҢШ§ ЪҜЩҲЫҢШ§) ШЁШұШҜШ§ШұЫҢШҜ. ЩҮЩ…ЫҢШҙЩҮ ЩҶЫҢШ§ШІ ЩҶЫҢШіШӘ Ш§ШІ ШӘШ№ШұЫҢЩҒ Щ…ШіШӘЩӮЫҢЩ…Ш§ Ш§ШіШӘЩҒШ§ШҜЩҮ Ъ©ЩҶЫҢШҜ. Ш§ЪҜШұ ШЁЩҮ ЩҫШ§ШұШ§ЪҜШұШ§ЩҒ ШҜЩҲЩ… ШөЩҒШӯЩҮЩ” ЫІЫұЫ¶ Ъ©ШӘШ§ШЁ ЩҶЪҜШ§ЩҮ Ъ©ЩҶЫҢШҜ ЫҢЪ© ШҙШұШ· ЩҮЩ…вҖҢШ§ШұШІ ШЁШұШ§ЫҢ ШЁЩҮвҖҢШ·ЩҲШұ Ъ©Ш§Щ…Щ„ Ъ©Ш§ЩҮШҙвҖҢЩҫШ°ЫҢШұ ШЁЩҲШҜЩҶ ЫҢЪ© ЩҶЩ…Ш§ЫҢШҙ ШҜШ§ШҜЩҮвҖҢШ§ШіШӘ ЩҲ ШўЩҶ ЩӮШ·ШұЫҢвҖҢШЁЩ„ЩҲЪ©ЫҢ ШҙШҜЩҶ Щ…Ш§ШӘШұЫҢШі ЩҶЩ…Ш§ЫҢШҙ Ш§ШіШӘ!
ШЁЫҢШ§ЫҢЫҢШҜ Щ…ШҜЩҲЩ„Щ…Ш§ЩҶ ШұШ§ ЩҒШ¶Ш§ЫҢ ШЁШұШҜШ§ШұЫҢ
$\mathbb{C}^2$
ШЁШұШҜШ§ШұЫҢЩ…. ЩҶЩ…Ш§ЫҢШҙЫҢ ШұШ§ ШҜШұ ЩҶШёШұ ШЁЪҜЫҢШұЫҢШҜ Ъ©ЩҮ Щ…Ш§ШӘШұЫҢШіШҙ ШЁЩҮ ШҙЪ©Щ„ ШІЫҢШұ ШҙЩҲШҜ.
$$\begin{bmatrix}1 & 1\\ 0 & 1\end{bmatrix}$$
Ш§ЪҜШұ ЩӮШұШ§Шұ ШЁШ§ШҙШҜ ЩҶЩ…Ш§ЫҢШҙЩ…Ш§ЩҶ ШЁЩҮ Ш·ЩҲШұ Ъ©Ш§Щ…Щ„ Ъ©Ш§ЩҮШҙвҖҢЩҫШ°ЫҢШұ ШЁШ§ШҙШҜ ШЁШ§ЫҢШҜ ШЁШӘЩҲШ§ЩҶ ШІЫҢШұЩ…Ш§ШӘШұЫҢШівҖҢЩҮШ§ЫҢ Щ…ШұШЁШ№ЫҢ Ш§Ъ©ЫҢШҜШ§ Ъ©ЩҲЪҶЪ©ШӘШұ ЫҢШ§ЩҒШӘ Ъ©ЩҮ Щ…Ш§ШӘШұЫҢШі ЩӮШ·ШұЫҢ-ШЁЩ„ЩҲЪ©ЫҢ ШӘШҙЪ©Щ„ЫҢвҖҢШҙШҜЩҮ ШЁШ§ ШўЩҶЩҮШ§ Щ…ШӘШҙШ§ШЁЩҮ ШЁЩҮ Щ…Ш§ШӘШұЫҢШі ШЁШ§Щ„Ш§ ШҙЩҲШҜ. ЪҶЩҲЩҶ Щ…Ш§ШӘШұЫҢШіЩ…Ш§ЩҶ ШҜЩҲ ШҜШұ ШҜЩҲ Ш§ШіШӘ ЩҫШі ШӘЩҶЩҮШ§ ШӯШ§Щ„ШӘ Щ…Щ…Ъ©ЩҶ ШЁШұШ§ЫҢ Щ…Ш§ШӘШұЫҢШівҖҢЩҮШ§ЫҢ Щ…ШұШЁШ№ЫҢ Ш§Ъ©ЫҢШҜШ§ Ъ©ЩҲЪҶЪ©ШӘШұ ЫҢЪ© ШҜШұ ЫҢЪ© Щ…ЫҢвҖҢШҙЩҲШҜ. ЫҢЪ© Щ…Ш§ШӘШұЫҢШі ШҜЩҲ ШҜШұ ШҜЩҲ Ъ©ЩҮ ШЁЩҮ ШәЫҢШұ Ш§ШІ ШҜЩҲ Щ…Ш§ШӘШұЫҢШі ЫҢЪ© ШҜШұ ЫҢЪ© ШҜШұ ЩӮШ·ШұШҙШҢ ШҜШұ ШЁЩӮЫҢЩҮЩ” Ш¬Ш§ЩҮвҖҢЩҮШ§ ШөЩҒШұ ШҜШ§ШұШҜ ШҜШұ ЩҲШ§ЩӮШ№ ЫҢЪ© Щ…Ш§ШӘШұЫҢШі ЩӮШ·ШұЫҢ ЩҶЫҢШІ ЩҮШіШӘ. ЩҫШі Щ…ШіШЈЩ„ЩҮ ШӘШЁШҜЫҢЩ„ Щ…ЫҢвҖҢШҙЩҲШҜ ШЁЩҮ Ш§ЫҢЩҶЪ©ЩҮ ШўЫҢШ§ Щ…Ш§ШӘШұЫҢШі ЩӮШ·ШұЫҢвҖҢШ§ЫҢ Щ…ШӘШҙШ§ШЁЩҮ ШЁЩҮ Щ…Ш§ШӘШұЫҢШі ЩҶЩ…Ш§ЫҢШҙЩ…Ш§ЩҶ ШҜШ§ШұЫҢЩ…Шҹ Ш§ЫҢЩҶ ШҜЩӮЫҢЩӮШ§ ЩҮЩ…Ш§ЩҶ Ш§ШөШ·Щ„Ш§Шӯ В«ЩӮШ·ШұЫҢвҖҢШҙШҜЩҶЫҢ ШЁЩҲШҜЩҶВ» Ш§ШіШӘ! Ш§ШІ Ш¬ШЁШұШ®Ш·ЫҢ ШЁЩҮ ЫҢШ§ШҜ ШўЩҲШұЫҢШҜ Ъ©ЩҮ ЪҶЪҜЩҲЩҶЩҮ ЩӮШ·ШұЫҢвҖҢШҙШҜЩҶЫҢ ШЁЩҲШҜЩҶ ШұШ§ ШЁШұШұШіЫҢ Щ…ЫҢвҖҢЪ©ШұШҜЫҢШҜ. Ш§ЫҢЩҶШ¬Ш§ Щ…ШЁШӯШ« ЩӮШ·ШұЫҢвҖҢШҙШҜЩҶЫҢ ЩҲ Щ…Ш«Щ„Ш«ЫҢвҖҢШҙШҜЩҶЫҢ ЩҲ ЩӮШ·ШұЫҢвҖҢШЁЩ„ЩҲЪ©ЫҢвҖҢШҙШҜЩҶЫҢ ШұШ§ ШҜШұШі ЩҶЩ…ЫҢвҖҢШҜЩҮЫҢЩ… ЩҲ ЩҫЫҢШҙвҖҢЩҒШұШ¶ ЩҒШұШҜЫҢ Ъ©ЩҮ ЩҶШёШұЫҢЩҮЩ” ЩҶЩ…Ш§ЫҢШҙ Щ…ЫҢвҖҢШ®ЩҲШ§ЩҶШҜ ШЁШ§ЫҢШҜ Ш¬ШЁШұШ®Ш·ЫҢ ШұШ§ ШЁШҜШ§ЩҶШҜ. ЪҶЫҢШІЫҢ Ъ©ЩҮ ШҜШұ Щ…Ш§ШӘШұЫҢШі ЩҶЩ…Ш§ЫҢШҙЩ…Ш§ЩҶ ШҜШ§ШұЫҢЩ… Ш§ЫҢЩҶ Ш§ШіШӘ Ъ©ЩҮ ЫҢЪ© Щ…Ш§ШӘШұЫҢШі ШЁШ§Щ„Ш§Щ…Ш«Щ„Ш«ЫҢ Ш§ШіШӘ ЩҫШі Щ…ЩӮШҜШ§Шұ ЩҲЫҢЪҳЩҮвҖҢЩҮШ§ЫҢШҙ Ш№ЩҶШөШұЩҮШ§ЫҢ ШұЩҲЫҢ ЩӮШ·Шұ Ш§ШөЩ„ЫҢвҖҢШ§Шҙ ЩҮШіШӘЩҶШҜ Ъ©ЩҮ ШӘЩҶЩҮШ§ ЫҢЪ© Ш№ШҜШҜ ЫҢШ№ЩҶЫҢ ЫҢЪ© Ш§ШіШӘ. Ш§ШІ ШўЩҶШ¬Ш§ Ъ©ЩҮ ЪҶЩҶШҜШ¬Щ…Щ„ЩҮвҖҢШ§ЫҢ Щ…ШҙШ®ШөЩҮЩ” ЫҢЪ© Щ…Ш§ШӘШұЫҢШі ШЁЩҮ ШҙЪ©Щ„ Ш¶ШұШЁ
$x-\lambda$
ЩҮШ§ Ъ©ЩҮ
$\lambda$
Щ…ЩӮШҜШ§Шұ ЩҲЫҢЪҳЩҮЩ” Щ…Ш§ШӘШұЫҢШі Ш§ШіШӘ Щ…ЫҢвҖҢШЁШ§ШҙШҜ ЩҲ Ш§ЫҢЩҶ Ш№Ш§Щ…Щ„вҖҢЩҮШ§ ШЁЩҮ ШӘШ№ШҜШ§ШҜ ШӘЪ©ШұШ§Шұ Щ…ЩӮШҜШ§Шұ ЩҲЫҢЪҳЩҮ ШҜШұ Ш¶ШұШЁ ШёШ§ЩҮШұ Щ…ЫҢвҖҢШҙЩҲЩҶШҜ ЩҫШі ЪҶЩҶШҜШ¬Щ…Щ„ЩҮвҖҢШ§ЫҢ Щ…ШҙШ®ШөЩҮЩ” Щ…Ш§ШӘШұЫҢШі ЩҶЩ…Ш§ЫҢШҙЩ…Ш§ЩҶ ШЁШұШ§ШЁШұ Ш§ШіШӘ ШЁШ§
$(x-1)^2$
ЩӮШ¶ЫҢЩҮвҖҢШ§ЫҢ ШҜШ§ШҙШӘЫҢЩ… Ъ©ЩҮ ЫҢЪ© Щ…Ш§ШӘШұЫҢШі ШұЩҲЫҢ Ш§Ш№ШҜШ§ШҜ Щ…Ш®ШӘЩ„Ш· ЩӮШ·ШұЫҢ ШҙШҜЩҶЫҢ Ш§ШіШӘ Ш§ЪҜШұ ЩҲ ШӘЩҶЩҮШ§ Ш§ЪҜШұ ЪҶЩҶШҜШ¬Щ…Щ„ЩҮвҖҢШ§ЫҢ Ъ©Щ…ЫҢЩҶ ШўЩҶ ЪҶЩҶШҜШ¬Щ…Щ„ЩҮвҖҢШ§ЫҢвҖҢШ§ЫҢ Ъ©Ш§ЩҮШҙвҖҢЫҢШ§ЩҒШӘЩҮ ШЁШ§ШҙШҜ ЫҢШ№ЩҶЫҢ ШӘЩҲШ§ЩҶ Ш№Ш§Щ…Щ„вҖҢЩҮШ§ЫҢ Ш®Ш·ЫҢвҖҢШ§Шҙ ШҜШұ ШӘШ¬ШІЫҢЩҮвҖҢШ§Шҙ ШЁШұШ§ШЁШұ ЫҢЪ© ШЁШ§ШҙШҜ. Ш§ШІ Ш·ШұЩҒЫҢ ЪҶЩҶШҜШ¬Щ…Щ„ЩҮвҖҢШ§ЫҢ Ъ©Щ…ЫҢЩҶ ЩҶЫҢШІ ЪҶЩҶШҜШ¬Щ…Щ„ЩҮвҖҢШ§ЫҢ Щ…ШҙШ®ШөЩҮ ШұШ§ Щ…ЫҢвҖҢШҙЩ…Ш§ШұШҜ ЩҫШі ЩҫШұШіШҙ Ш§ЫҢЩҶЪ©ЩҮ В«ШўЫҢШ§ Щ…Ш§ШӘШұЫҢШі ЩҶЩ…Ш§ЫҢШҙ Щ…Ш§ ЩӮШ·ШұЫҢвҖҢШҙШҜЩҶЫҢ Ш§ШіШӘ ЫҢШ§ Ш®ЫҢШұШҹВ» ЩҮЩ…вҖҢШ§ШұШІ Щ…ЫҢвҖҢШҙЩҲШҜ ШЁШ§ Ш§ЫҢЩҶЪ©ЩҮ В«ШўЫҢШ§ ЪҶЩҶШҜШ¬Щ…Щ„ЩҮвҖҢШ§ЫҢ Ъ©Щ…ЫҢЩҶ ШўЩҶ ШЁШұШ§ШЁШұ ШЁШ§
$x-1$
Ш§ШіШӘ ЫҢШ§ Ш®ЫҢШұШҹВ» ЩҲ ШЁШұШ§ЫҢ ЪҶЪ© Ъ©ШұШҜЩҶ ШўЩҶ Ъ©Ш§ЩҒЫҢШіШӘ ШЁЩҮ Ш¬Ш§ЫҢ Щ…ШӘШәЫҢШұ
$x$
Щ…Ш§ШӘШұЫҢЩ…Ш§ЩҶ ШұШ§ ЩӮШұШ§Шұ ШҜЩҮЫҢЩ… ЩҲ ШЁШЁЫҢЩҶЫҢЩ… ШўЫҢШ§ ШөЩҒШұ Щ…ЫҢвҖҢШҙЩҲШҜ ЫҢШ§ Ш®ЫҢШұ.
$$\begin{bmatrix}1 & 1\\ 0 &1\end{bmatrix}-\begin{bmatrix}1 & 0\\ 0 & 1\end{bmatrix}=\begin{bmatrix} 0 & 1\\ 0 & 0\end{bmatrix}$$
Ъ©ЩҮ Щ…Ш§ШӘШұЫҢШі ШөЩҒШұ ЩҶЫҢШіШӘ. ЩҲ Ш§ЫҢЩҶ Ш§Ш«ШЁШ§ШӘ ШұШ§ ШӘЩ…Ш§Щ… Щ…ЫҢвҖҢЪ©ЩҶШҜ.