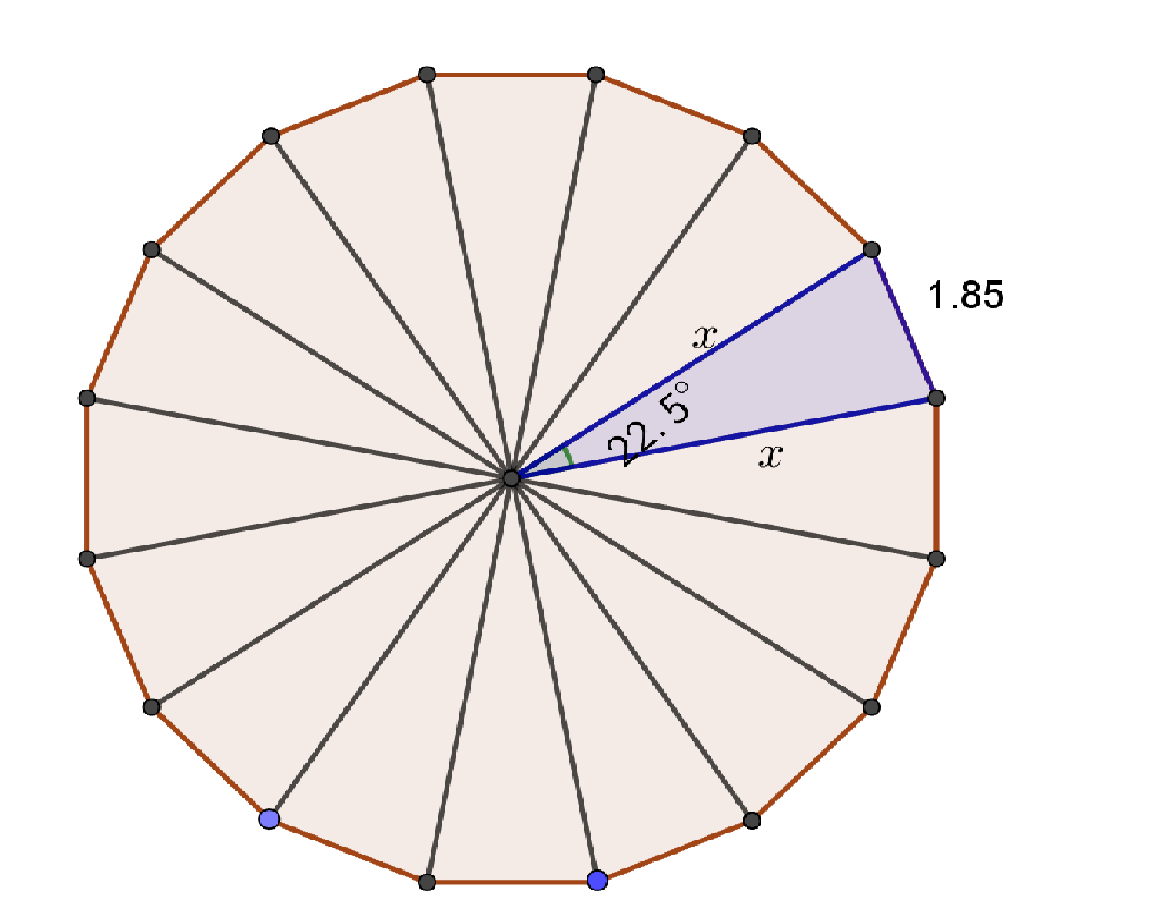
$(1.85)^{2}=2x^{2}-2x^{2}cos(22.5)^{ \circ }=2x^{2}(1-cos(22.5))$
باتوجه به $cos(45)^{ \circ }=2cos^{2}(22.5)^{ \circ }-1$است پس:
$ x^{2}\simeq 22.48 $$cos(22.5)^{ \circ }= \frac{\sqrt{2+\sqrt{2}}}{2} \Longrightarrow $
و$sin(22.5)^{ \circ }= \frac{\sqrt{2-\sqrt{2}}}{2}$
درنتیجه$ s=16 \times \frac{1}{2}x^{2}sin(22.5)^{ \circ } \simeq 68.82$