حجم کره به شعاع $r$ برابر است با $\frac{4}{3}\pi r^3$. شعاع گوی، ۳ است پس حجمش $36\pi$ واحد مکعب میشود.
استوانه با شعاع قاعدهٔ $R$ و ارتفاع $h$ دارای حجمِ $\pi R^2h$ است. شعاع قاعدهٔ ظرف استوانهای، ۴ و ارتفاعش ۷ است. پس حجمش $112\pi$ واحد مکعب است. حجم اشغال شده از آن با آب برابر با حجم استوانه با قاعدهٔ یکسان ولی ارتفاع ۳ است پس این حجمِ اشغال شده $48\pi$ است.
اکنون گوی را داخل ظرف بیندازید، مقدار فضای اشغال شده برابر با حجم آب بعلاوهٔ حجم گوی است یعنی $84\pi$.
اگر فرض کنیم گوی به طور کامل داخل آب برود آنگاه یک استوانه با قاعدهٔ دایرهای با شعاع ۴ و حجمِ $84\pi$ واحد مکعب داریم. یک استوانه با قاعدهٔ یکسان و چنین حجمی نیاز به چه اندازهارتفاعی دارد؟ $\frac{84\pi}{16\pi}=5.25$ پس ارتفاع آب پس از ورودِ گوی برابر با این عدد است که ۲/۲۵ واحد از پیش از ورودِ گوی بالاتر است.
چون قطر کره ۶ واحد است و ۵/۲۵ از آن کمتر است پس حرف شما درست است و فرض اینکه گوی به طور کامل به زیر آب برود ناممکن است.
اینک پاسخ درست چه میباشد؟ بیاییم ارتفاع جدید آب که فعلا آن را نمیدانیم، $h_0$ بنامیم. با استفاده از انتگرال حجم شکل زیر برابر است با:
$$\pi R^2h_0+\int_{h_0-r}^{2r-r}\pi (\sqrt{r^2-x^2})^2dx$$
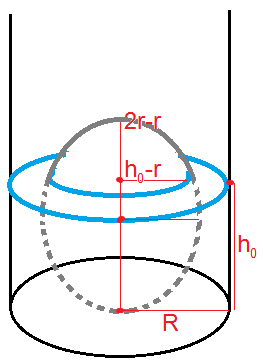
چون این حجم باید برابر با جمع حجم گوی و آب شود داریم؛
$$84\pi=(16\pi h_0)+\Big((18\pi)-\big(\pi(-\frac{(h_0-3)^3}{3}+9h_0-27)\big)\Big)$$
که با سادهسازی یک معادلهٔ درجهٔ سه داریم:
$$\pi(\frac{1}{3}h_0^3-3h_0^2+16h_0-48)=0$$
که دو ریشهٔ مختلط و یک ریشهٔ حقیقی دارد. ریشهٔ حقیقی با تقریب دو رقم اعشار برابر است با 5.11. پس ارتفاع آب تقریبا 2/11 واحد بالا میآید نه ۲/۲۵.