درباره رابطه بین اپسیلون و دلتا در حد

Question

سلام در عکس پایین من اثبات قضیه حد ضرب دو تابع رو آوردم .

اصلا با اثبات قضیه کاری ندارم بحث من سر اپسیلون و دلتا است. در قسمتی از این اثبات آمده است:

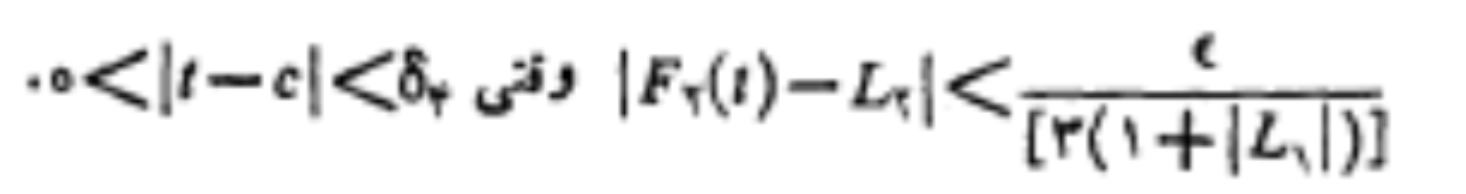
اگر بخواهیم این حد را روی نمودار نشان دهیم به شکل زیر است:

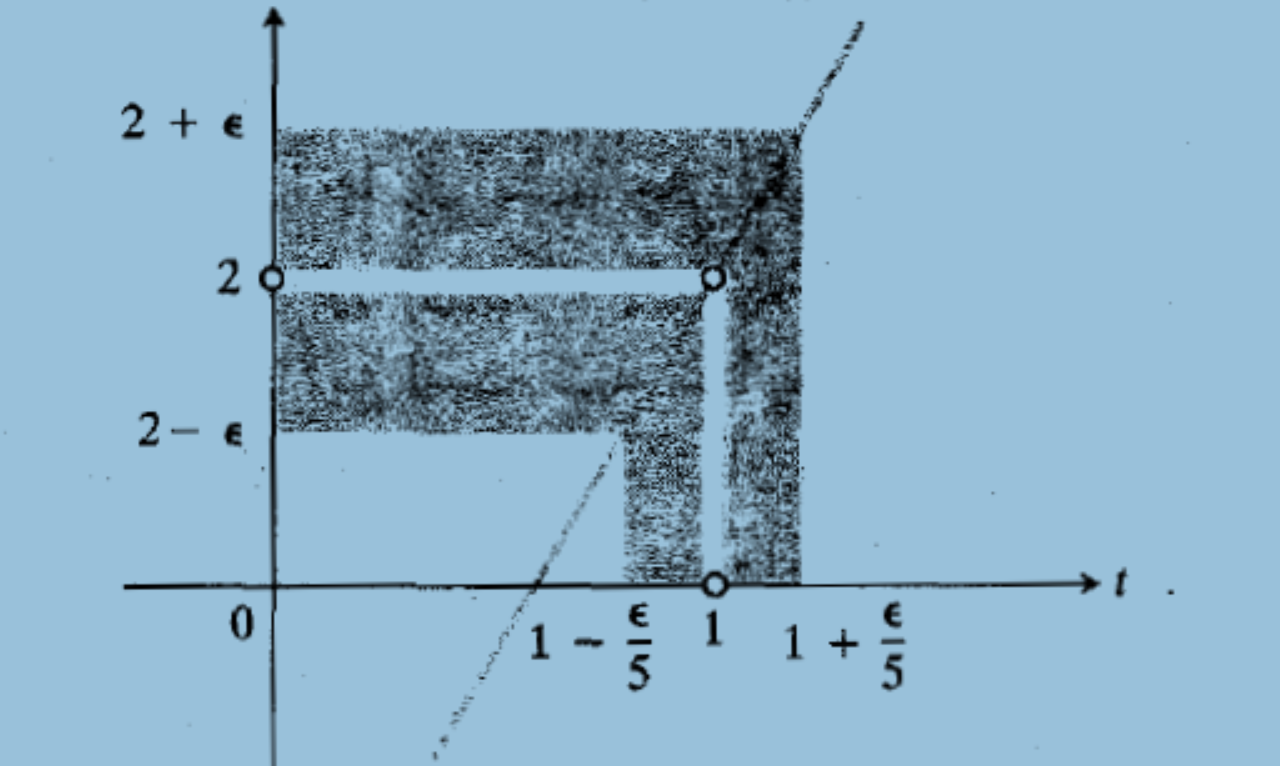
منظور من از آوردن این شکل این است که مقادیر f تمامی tهایی که در بازه c+ \delta وc- \delta قرار دارند تمامی فضای بین L+ \epsilon وL- \ epsilonرا پر می کنند. در آخر این اثبات اپسیلون سوم رو +اپسیلون سوم+اپسیلون سوم کرده و به این رسیده.

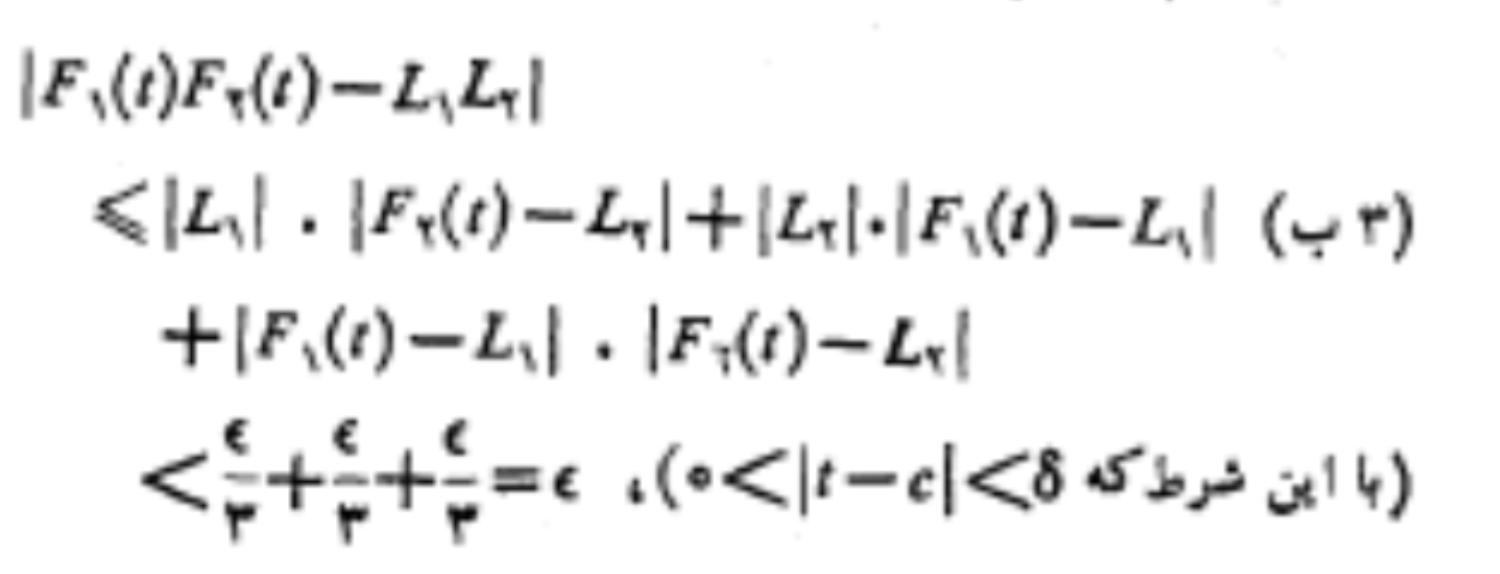
ذهنیت من این است که اگر بخواهیم این حد را روی نمودار نشان دهیم به شکل زیر در می آید.

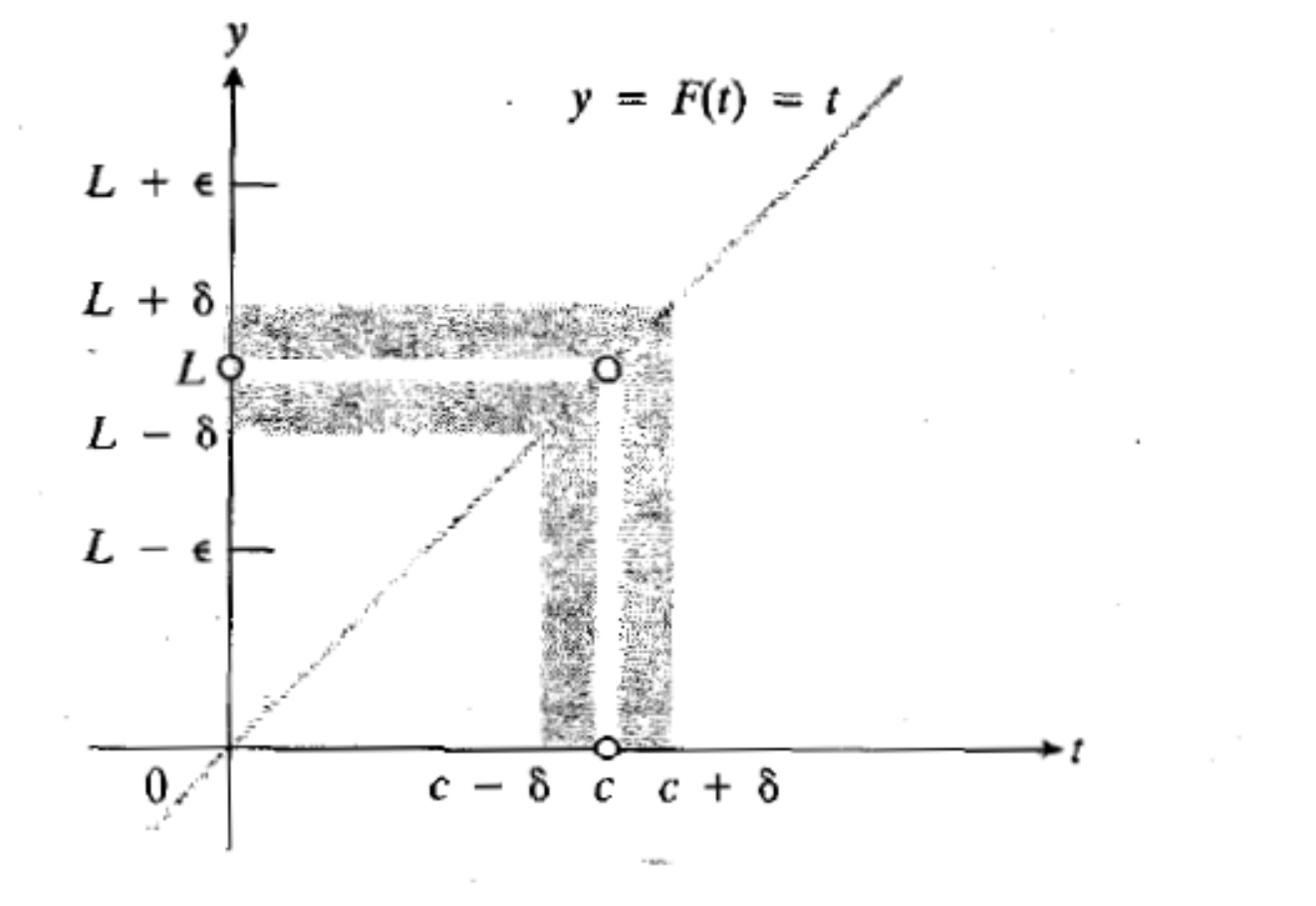
منظورم این است که مقادیر f تمامی tهایی که در بازه c+ \delta وc- \delta قرار دارند تمامی فضای بین L+ \epsilon وL- \epsilon را پر نمی کنند و قسمتی از بازهL+ \epsilon وL- \epsilon فاقد مقادیر f است. دلیل من برای این ذهنیتم این است که اپسیلون سوم +اپسیلون سوم+اپسیلون سوم بزرگ تر است از اپسیلون سوم و علاوه بر آن \delta یی که در نا معادله دوم آمده کوچکتر است از \delta یی که در معادله اول آمده زیرا این دراثبات بیان شده است. من اصلا با این کاری ندارم که می توانیم هر چقدر که می خواهیم \epsilon را کوچک بگیریم. ذهنیت من این است که اگر در معادله اولی خود \delta را یک عدد فرضی در نظر بگیرم که می توانیم این کار را بکنیم و آن را به f بدهیم f هم به ما \epsilon را میدهد. اما اگر همین کار را در معادله دوم انجام دهیم مقدار خروجی f درون بازه L+ \epsilonوL- \ epsilon قرار دارد. می خواستم ببینم که آیا ذهنیت من درست است یا نه. ممنون میشم راهنمایی کنید.

Comments

چرا برچسب نرم‌افزار برای این پرسش انتخاب کرده‌اید؟ من چیزی که اشاره‌ای به نرم‌افزاری داشته‌باشد نمی‌بینم. بعلاوه برای عبارت‌های ریاضی‌تان ظاهرا علامت‌های دلار را فراموش کرده‌اید. و اگر چیزی را از جایی برمی‌دارید بد نیست که به مرجع اشاره کنید، مثلا تصویر فلان یا متن فلان از صفحهٔ فلان کتاب فلان را در زیر آورده‌ام. چون متنی که آوردید از اثر دیگری است و اثبات یا نوشته یا تصویر رسم‌شده بوسیلهٔ خودتان نیست و جزو حقوق صاحبِ اثر و اخلاق آکادمی است که نام اثرش را بیاورید.

Answer 1

به نظر می رسد مشکل شما در تعریف اپسیلوت-دلتای حد هست. بنابر تعریف حد $\lim_{x\to c}f(x)=L$ یعنی $$\forall \epsilon>0\quad \exists \delta>0 :\quad (0< |x-c|< \delta\implies |f(x)-L|< \epsilon)$$

برای هر اپسیلون دلخواه شما بتوانید دلتایی(وابسته به $c$ و $\epsilon$) بیابید که اگر $x$ در همسایگی محذوف دلتای $c$ (یعنی $0< |x-c|< \delta$ ) واقع شود آنگاه مقادیر $f(x)$ در همسایگی اپسیلون $L$ (یعنی $|f(x)-L|< \epsilon$ ) قرار گیرند. لازم نیست حتما مقادیر $f(x)$ تمامی فضای همسایگی اپسیلون $L$ را دربرگیرد بلکه کافی است زیرمجموعه ای از آن باشد. به عبارت دیگر اگر همسایگی محذوف دلتای $c$ را با $U$ و همسایگی اپسیلون $L$ را با $V$ نمایش دهیم آنگاه باید $f(U)\subseteq V$ و ذهنیت شما که فکر می کنید باید حتما $f(U)=V$ اشتباه است.