بررسی محل برخورد دو سهمی

Question

سلام میخواستم بدونم چجوری میشه فهمید که دو تا سهمی در چه نقاطی باهم تماس دارن؟ چجوری بفهمیم که دوتا سهمی متقاطع هستن یا نه؟ اگر هستن از کجا بفهمیم توی یک نقطه یا دو نقطه متقاطعن؟

Answer 1

خب معادله تلاقی تشکیل بدید :$ a x^{2}+bx+c= a' x^{2}+ b'x+c' $

اگر دلتا بزرگتر از صفر بود در دونقطه هم دیگر رو قطع می کنند

اگر کوچکتر از صفر بود متقاطع نیستند

Comments

@fardinffa الزامی ندارد که به صورت پیش‌فرض معادلهٔ سهمی‌تان به شکل $y=ax^2+bx+c$ نوشته شود. سهمی‌تان می‌تواند افقی یا حتی با زاویهٔ دیگری باشد. بعلاوه معادله‌ای که نوشتید درجه ۲ است که حداکثر ۲ پاسخ می‌تواند داشته‌باشد، ولی می‌توان دو سهمی برداشت که در چهار نقطه با درازاها (طول‌ها)ی متفاوت باشند.

Answer 2

برای این که بخواین بفهمین در چه نقاطی باهم تقاطع دارند . روشی که دوست عزیز فرستادن کامل ترینه.

اما اگر به منظور دانستن تعداد نقاط باشه یا این که ایا متقاطع هستند یا خیر. روش سریع تری که وجود داره. رسم دو شکل است. به طوری که هر دو تابع مورد نظر رو میکشین و نگاه کنید ایا برخورد دارند یا خیر.

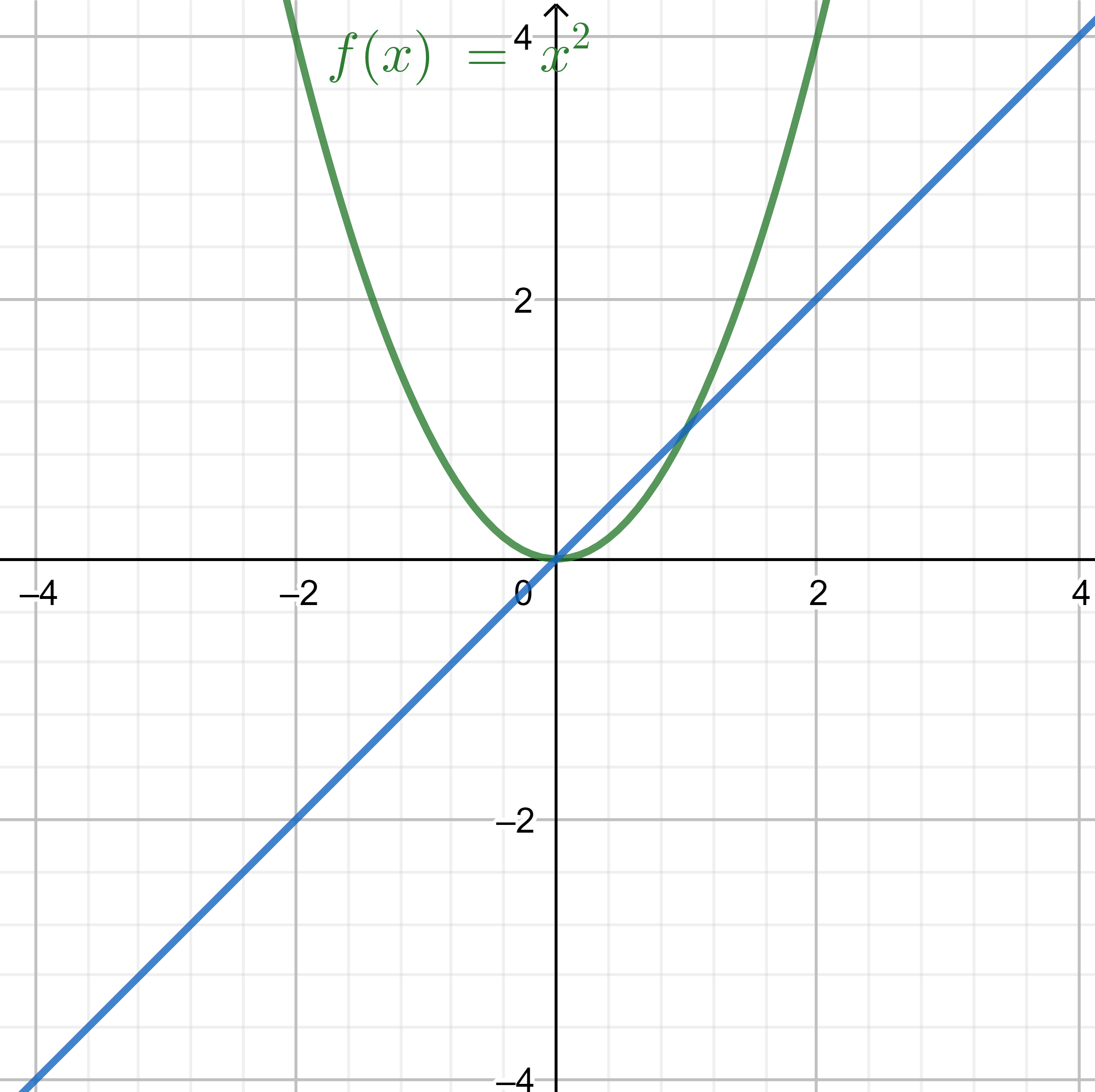
مثال تابع $ x^{2} $ و خط y=x

به روشی که دوست عزیز توضیح دادند اینگونه میشود که $x= x^{2} => x^{2}-x=0=>x(x-1)=0===>x=0,1 $ پس در دو نقطه 0.1 قطع میکنند. حال اگر به ما گفته بودن تعداد نقاط به راحتی با رسم شکل میفهمیم که در 2 نقطه برخورد دارند

مثل شکل زیر

Comments

از بخش رسم نمودار می توانید برای چنین نمودارهایی استفاده کنید:
https://math.irancircle.com/geogebra

---

تشکر استاد. ممنونم ازتون