به نام خدا.
پاسخ آقای @MSS صحیح است و من فقط در این جا توضیح می دهم که چه کار کرده اند. @good4us و @nana1164
پاره خط$EF$ به طول $x$ موازی با دو قاعده ذوزنقه $ABCD$ است. حال از $C$ عمودی بر $BD$ وارد می کنیم تا نقاط زیر پدید آیند:
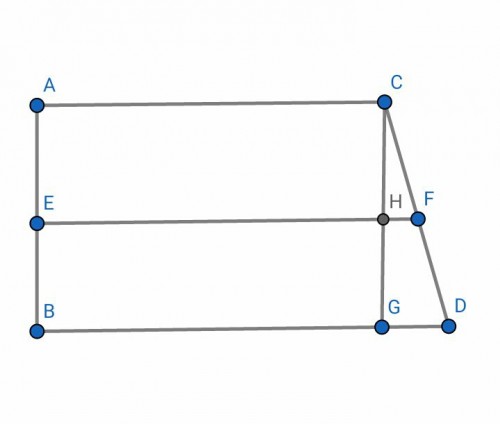
فرض کنید که $BE=y$ باشد. $FH=x-35$ و $GD=21$ و $CH=28-y$ می باشد. با توجه به اینکه در مثلث $CGD$ دو پاره خط $FH$ با $DG$ موازی است، پس:
$ \frac{CH}{CG} = \frac{FH}{DG} \Longrightarrow \frac{28-y}{28} = \frac{x-35}{21} \Longrightarrow y= \frac{224-4x}{3} $
که با قرار دادن در معادله ی آقای @MSS به جواب خواهید رسید.