ШЁЩҶШ§Щ… Ш®ШҜШ§.Ш·ШЁЩӮ ШҙЪ©Щ„ ШҜШ§ШұЫҢЩ… 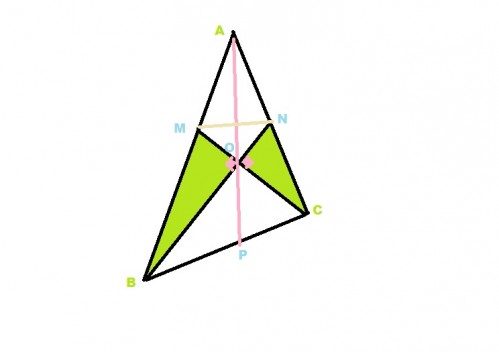 $$AP^2=(3OP)^2=9OP^2
$$Ш·ШЁЩӮ Ш®Ш§ШөЫҢШӘ Щ…ЫҢШ§ЩҶЩҮ ЩҮШ§ЩҲЪҶЩҲЩҶ Щ…Ш«Щ„Ш« OBC ЩӮШ§ШҰЩ… Ш§Щ„ШІШ§ЩҲЫҢЩҮ Ш§ШіШӘ Щ…ЫҢШ§ЩҶЩҮ ЩҲШ§ШұШҜ ШЁШұ ЩҲШӘШұ ЩҶШөЩҒ ЩҲШӘШұШ§ШіШӘ ЫҢШ№ЩҶЫҢ
$$AP^2=(3OP)^2=9OP^2
$$Ш·ШЁЩӮ Ш®Ш§ШөЫҢШӘ Щ…ЫҢШ§ЩҶЩҮ ЩҮШ§ЩҲЪҶЩҲЩҶ Щ…Ш«Щ„Ш« OBC ЩӮШ§ШҰЩ… Ш§Щ„ШІШ§ЩҲЫҢЩҮ Ш§ШіШӘ Щ…ЫҢШ§ЩҶЩҮ ЩҲШ§ШұШҜ ШЁШұ ЩҲШӘШұ ЩҶШөЩҒ ЩҲШӘШұШ§ШіШӘ ЫҢШ№ЩҶЫҢ
$$AP^2=9OP^2=9( \frac{1}{2}BC)^2= \frac{9}{4} BC^2= \frac{9}{4} (2MN)^2=9MN^2=
$$
$$9(OM^2+ON^2)=9{( \frac{1}{3} MC)^2+9( \frac{1}{3} NB)^2}=MC^2+NB^2$$
ШЁЩҶШ§ШЁШұШ§ЫҢЩҶ ШҜШ§ШұЫҢЩ…: $$AP^2=MC^2+NB^2$$