زمانی که یک آزمایش با دو برآمد دارید مانند پرتاب سکه که شیر یا خط بیاید، آنگاه متغیر تصادفی تعداد دفعههای پرتاب تا دیدن نخستین برآمد خواستهشده یک متغیر تصادفی گسستهٔ هندسی نامیده میشود. اگر این متغیر را با $X$ نمایش دهید آنگاه گاهی آن را تعداد پرتابها تا نخستین پیروزی با احتساب خود پرتاب پیروزمند میگیرند و گاهی تعداد پرتابهای شکستخورده بدون احتساب خود پرتاب پیروزشده میگیرند. در هر دو صورت فرمولها یکسان هستند، تنها فرق این است که یکی یک واحد کمتر از دیگری مقدار دارد. در اینجا خود پرتاب آخر را نیز میشماریم. فرض کنید حالت خواستهشده که آن را پیروزی صدا میکنیم با احتمال $p$ که عددی بین صفر و یک است رُخ میدهد که در نتیجه حالت دیگر که آن را شکست صدا میزنیم با احتمال $1-p$ روی میدهد. اینکه در $x$اُمین پرتاب پیروزی برای نخستین بار رخ بدهد یعنی اینکه در $x-1$ پرتاب آغازین باید شکست رخ داده باشد و سپس در $x$اُمین پرتاب یک پیروزی رخ دهد. این کار بنا به اصل ضرب احتمالش برابر است با
$$\underset{(x-1)-\text{times}}{\underbrace{(1-p)\times\cdots (1-p)}}\times p=(1-p)^{x-1}p$$
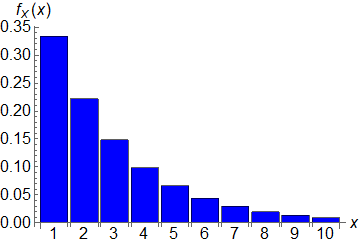
به تابعی که هر مقدار ممکن برای متغیر تصادفی گسستهمان را به احتمال روی دادنش مینگارد تابع پخش چگالی (توزیع چگالی) میگویند و معمولا با $f_X(x)$ نمایش میدهند. پس برای این پرسش داریم $f_X(x)=(\frac{2}{3})^{x-1}(\frac{1}{3})$. کشیدن نمودار برای آن نیز کاری ندارد، یک نمودار میلهایِ بسیار ساده دارید. با نرمافزار Mathematica این نمودار را میتوانید با دستور زیر بکشید.
BarChart[<|Table[i->(1-1/3)^(i-1)*1/3,{i,1,10}]|>,ChartLabels->Automatic,ChartStyle->Blue,AxesLabel->{ToExpression["x",TeXForm,HoldForm],ToExpression["f_X(x)",TeXForm,HoldForm]},LabelStyle->Directive[Black,16]]
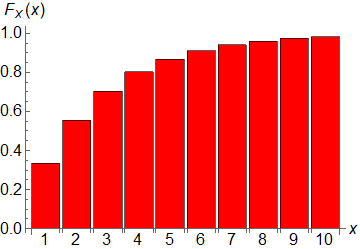
اکنون تابع پخش انباشتگی (توزیع تجمعی). تابع پخش انباشتگی به هر مقدار برای متغیر تصادفیمان جمع احتمال رخ دادن همهٔ مقدارهای کوچکتر یا مساویاش را مینگارد. یعنی اگر احتمال رخ دادن پیشمادی (پیشامد یک زیرمجموعه از فضای نمونه است که میتواند ناتکعضوی نیز باشد) را با $P$ نمایش دهیم و تابع پخش انباشتگی را با $f_x(X)$، آنگاه داریم:
$$F_X(x)=P(\lbrace y\in\Omega\mid y\leq x\rbrace)$$
که در اینجا چون $\Omega=\mathbb{N}$ میشود
\begin{align}
F_X(x) &=P(\lbrace y\in\mathbb{N}\mid y\leq x\rbrace)\\
&=P(\lbrace 1,2,\cdots,x\rbrace)\\
&=\sum_{i=1}^xf_X(i)
\end{align}
پس با داشتن ضابطهٔ تابع پخش چگالی میتوان ضابطهٔ تابع پخش انباشتگی را نیز بدست آورد. راه دیگری برای محاسبهٔ تابع پخش انباشتگی به کمک تابع پخش چگالی نیز هست که از سمت برعکش روش بالا اقدام میکند. چون میدانیم که جمع مقدارهای تابع چگالی یک میشود یا به عبارت دیگر تابع انباشتگی برای بزرگترین مقدار ممکن (یا حد آن زمانی که $x$ به بینهایت میل میکند) برابر ۱ است میتوان گفت
\begin{align}
F_X(x) &=P(\lbrace y\in\Omega\mid y\leq x\rbrace)\\
&=P(\Omega-\lbrace y\in\Omega\mid y\leq x\rbrace)\\
&=1-P(\lbrace y\in\Omega\mid y> x\rbrace)\\
&=1-P(\lbrace y\in\mathbb{N}\mid y> x\rbrace)\\
&=1-P(\lbrace x+1,x+2,\cdots\rbrace)\\
&=1-\sum_{i=x+1}^\infty f_X(i)
\end{align}
برای این پرسش خواهیم داشت
\begin{align}
F_X(x) &=1-\sum_{i=x+1}^\infty (\frac{2}{3})^{i-1}(\frac{1}{3})\\
&=1-\frac{(\frac{2}{3})^{(x+1)-1}(\frac{1}{3})}{1-\frac{2}{3}}\\
&=1-(\frac{2}{3})^x
\end{align}
راه دیگر برای محاسبهٔ تابع انباشتگی در این پرسش این است که توجه کنید که برای اینکه پیروزی در $x$ پرتاب نخست روی ندهد باید $x$ شکست داشته باشید که احتمالش $(\frac{2}{3})^x$ است. سپس اینکه پیروز در $x$ پرتاب نخست روی دهد یعنی متمم پیشامد پیشین پس احتمالش یک منهای احتمال پیشامد پیشین است یعنی $1-(\frac{2}{3})^x$. برای رسم نمودار تابع انباشتگی هم نیاز به انجام چیز عجیب و غریبی نیستید یک تابع با دامنهٔ گسسته دارید؟ چه نموداری مناسب است؟ نمودار میلهای. نمودار میلهای را چگونه رسم میکنیم؟ یکی یکی مقدار دهی میکنیم و برای چند مقدار میلهها را میکشیم. اگر هم میخواهید از نرمافزار استفاده کنید، دوباره دستور کشیدن آن به کمک نرمافزار Mathematica در زیر آوردهشدهاست.
BarChart[<|Table[i->1-(1-1/3)^i,{i,1,10}]|>,ChartLabels->Automatic,ChartStyle->Red,AxesLabel->{ToExpression["x",TeXForm,HoldForm],ToExpression["F_X(x)",TeXForm,HoldForm]},LabelStyle->Directive[Black,16]]