با درود و سپاس از سؤال خوبتان. ساده ترین توضیح درباره تفاوت دیفرانسیل و مشتق را میتوان در دو مرجع زیر یافت.
Differentiation is the first big idea in calculus. It’s the process of finding a derivative of a curve. And a derivative is just the fancy calculus term for a curve’s slope or steepness.
دیفرانسیل اولین ایده بزرگ در حسابان است. دیفرانسیل فرآیند یافتن مشتق یک منحنی است. و مشتق فقط یک واژه حسابانی فانتزی برای ضریب زاویه یا شیب یک منحنی است.
مرجع: Calculus Essentials For Dummies, Mark Ryan, John Wiley publisher, 2010, P:8
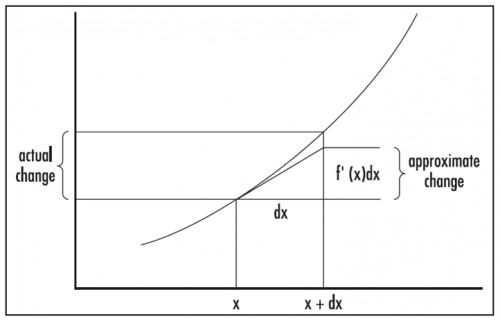
differential: Close to any point $x$, the graph of a differentiable function $y=f(x)$ is well approximated by a small straight-line segment tangent to the graph at $x$. The slope of this tangent line is the DERIVATIVE $f'(x)$. Using the symbol $dx$ to represent a small change in the $x$-variable, we see that the corresponding change in the $y$-variable is approximately $dy = f’ (x)dx$. The quantities $dx$ and $dy$ are called differentials.
دیفرانسیل: با هر نقطه نزدیک به $x$، نمودار تابع دیفرانسیلپذیر $y=f(x)$ بخوبی با پاره خط مستقیم کوچک مماس بر نمودار در $x$ تقریب زده میشود. شیب این خط مماس مساوی با مشتق $ f' (x)$ است. با استفاده از نماد $dx$ برای نمایش تغییر کوچک در متغیر $x$ ،می بینیم که تغییر متناظر در متغیر $y$ تقریباً مساویست با $dy = f'(x)dx$. کمیتهای $dx$ و $dy$ دیفرانسیل نامیده میشوند.
مرجع: Encyclopedia of Mathematics, James Tanton, 2005, P: 131 - 132
از مطالب فوق براحتی میتوان فهمید که مشتق یکی از محصولات دیفرانسیل است و مشتق را میتوان حاصل تقسیم دیفرانسیل $dy$ بر دیفرانسیل $dx$ نامید. دیفرانسیل، روابط بین متغیرمستقل $x$ و متغیر وابسته $y$ را بیان میکند درحالیکه مشتق، حاصل یکی از روابط دیفرانسیل است یعنی $y'= f'(x)= \frac{dy}{dx}$ و روابط دیفرانسیل لزوماً به مشتق منتهی نمیشود. مثال:
$ \frac{ d^{4}y }{d x^{4} } + \frac{2 d^{2}y }{d x^{2} }+y=8sinx-16cosx $
میتوان گفت رابطه دیفرانسیل با مشتق مانند رابطه تقسیم دو کمیت با حاصل تقسیم آنهاست. موفق باشید.