Question

اگر اضلاع یک مثلث قائم الزاویه تشکیل یک دنباله حسابی بدهند تحقیق کنید که قدرنسبت مساوی شعاع دایره محاطی مثلث است و خمس وتر.

Comments

@Mohammad.reza77 چرا اصلاً به تلاش خودتان اشاره نکردید؟ در این سایت و هر سایت پرسش و پاسخ ریاضیِ دیگری، در هنگام پرسش یک سؤال، باید به تلاش خودتان نیز اشاره کنید. تا اگر راه‌حل‌تان مشکلی دارد، بتوانیم به شما کمک کنیم.

---

@Mohammad.reza77 به غیر از نکته‌ای که @Math.Al اشاره کردند، در سمت چپ همین صفحه دست‌کم دو پرسش پیرامون سه‌گوش‌های قائم‌الزاویه با یال‌هایی که درازایشان تشکیل دنبالهٔ حسابی بدهد نشان داده‌شده‌است. پیش از ارسال پرسش به آنها سر زده‌اید؟ یک قسمت پرسش‌تان در یکی و قسمتی دیگر در دیگری پاسخ می‌گیرد.
https://math.irancircle.com/16235
https://math.irancircle.com/21651

Answer 1

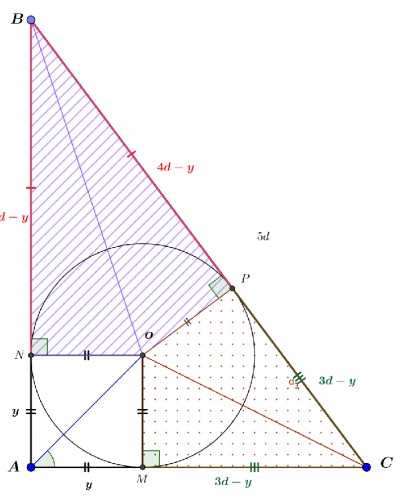
باتوجه به اینکه در مثلث قائم الزاویه $ABC$ اضلاع دنباله حسابی هستند میتوان آنها را $AC=x-d,AB=x,BC=x+d$ فرض کرد و بنابه فیثاغورس:

$$\color{blue}{(x-d)^2+d^2=(x+d)^2} \Rightarrow x=4d$$

وقتی نیمسازها را رسم کنیم که مرکز دایره محاطی حاصل میشود بدیهی است با رسم شعاع های وارد بر اضلاع مثلث(شعاع دایره محاطی) چهارضلعی $AMON$ مربع خواهدبود و وقتی یک ضلع آن را $y$ بنامیم و با توجه همنهشتی مثلث های دوبه دو مشخص (به حالت وتر و یک زاویه تند) در شکل نامگذاری ها را قید کردیم به این ترتیب :

$$4d-y+3d-y=5d \Rightarrow y=d \Rightarrow\color{red}{ OM=ON=OP=d= \frac{1}{5}BC} $$

Comments

Mohammad.reza77@ در تصویر $4d-y$ در بغل تصویر ناقص است.

Answer 2

اگر$a$,$a-d$،$a+d$اضلاع مثلث قائم الزاویه با وتر$a+d$باشند که$d$قدرنسبت تصاعد باشد طبق رابطه فیثاغورث داریم$$(a+d)^2=a^2+(a-d)^2$$که نتیجه می دهد$a=0$و$a=4d$که$a=0$قابل قبول نیست لذا اضلاع مثلث سه تایی$(a-d,a،a+d)$ با محیط$12d$و مساحت$ \frac{4d\times3d}{2}=6d^2 $خواهد بود.شعاع دایره محاصی برابر نسبت مساحت به نصف محیط است یعنی$$ \frac{s}{p} $$که $p$نصف محیط است. لذا شعاع دایره محاطی برابر است با$$ \frac{6d^2}{6d}=d $$یعنی شعاع دایره محاطی برابر قدر نسبت است که برابر خمس یا یک پنجم وترنیز هست.$$r= \frac{5d}{5} =d$$

Comments

AmirHosein@
سلام و سپاس از توجه تان. اصلاح شد.