به جای اینکه پاسخ دقیق و بستهٔ این انتگرال نامعین را بیابیم، تقریب بسط تیلور آن را مییابیم. ابتدا توجه کنید که اگر تابع $f(x)$ را به شکلِ زیر تعریف کنیم
$$f(x)=\int_0^xe^x\tan(x){\rm d}x$$
آنگاه این تابع در نقطهٔ $x=0$ برابر با صفر است و سپس با افزایش $x$ به صورت یکنوا افزایش مییابد (افزایشی اکید - صعودی اکید) تا در $x=\frac{\pi}{2}$ به بینهایت واگرا میشود و دارای مجانب عمودی میشود. برعکس اگر از $x=0$ به پُشت (عقب) حرکت کنیم باز تابع افزایش مییابد (اما اگر در جهت محور $x$ها نگاه کنیم باید بگوئیم کاهشی اکید - نزولی اکید - است) تا در $x=\frac{-\pi}{2}$ به مجانب عمودی بر بخوریم. پس من دامنهٔ $f(x)$ را به $(-\frac{\pi}{2},\frac{\pi}{2})$ تحدید میکنم. نمودار این تابع در این بازه در زیر آوردهشدهاست. توجه کنید که در هر دو سمت مجانب عمودی داریم (به کوتاهی-بلندی خم در شکل توجهی نکنید).
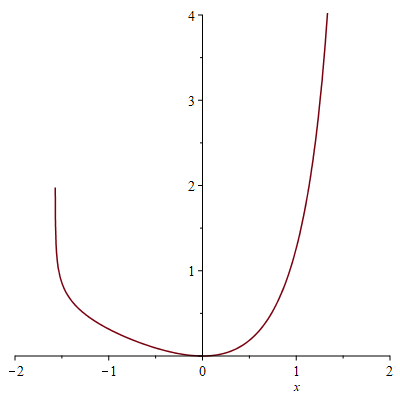
اکنون چون مقدار تابع در $x=0$ را میدانیم و مقدار مشتقهایش هم در این نقطه به راحتی محاسبه میشوند، بسط تیلور را پیرامون (در حول) این نقطه مینویسم (میتوانید پیرامون نقطههای دیگر بنویسید ولی آنگاه باید مقدار تابع و مشتقهایش را در آن نقطه پیدا کنید که نیاز به محاسبه دارد و به سادگی این نقطه نیست). برای مشتق یکُم از قانون لایبنتیز برای مشتق تابعهای انتگرالی استفاده میکنیم. اگر این قانون را فراموش کردهاید، اینجا مرورش میکنیم.
فرض کنید $f(x)=\int_{a(x)}^{b(x)}g(x,t){\rm d}t$ در این صورت داریم؛
$$\frac{{\rm d}g(x)}{{\rm d}x}=g(x,b(x))\frac{{\rm d}b(x)}{{\rm d}x}-g(x,a(x))\frac{{\rm d}a(x)}{{\rm d}x}+\int_{a(x)}^{b(x)}\frac{\partial g(x,t)}{\partial x}{\rm d}t$$
پس برای تابع پرسشِ کنونیمان داریم
$$\begin{align}
f'(x) &= e^x\tan(x)\Big(\frac{{\rm d}x}{{\rm d}x}\Big)-e^0\tan(0)\Big(\frac{{\rm d}0}{{\rm d}x}\Big)+\int_0^x\frac{\partial \Big(e^t\tan(t)\Big)}{\partial x}{\rm d}t\\
&= e^x\tan(x)-0+0\\
&= e^x\tan(x)
\end{align}$$
مشتقهای پسین را به راحتی بدون قانون لایبنتیس خودتان میتوانید محاسبه کنید برای نمونه
$$f''(x)=x^x\tan(x)+e^x\big(1+\tan^2(x)\big)$$
و سپس با جایگذاری در فرمول بسط تیلور در نقطهٔ $x=0$ تا جملهٔ جملهٔ توان چهارم داریم
$$f(x)\simeq\frac{1}{2}x^2+\frac{1}{3}x^3+\frac{1}{24}x^4+\mathcal{O}(x^5)$$
اما توجه کنید که نمیتوان گفت که تا چند جمله از این بسط را نیاز دارید تا مقدار تابع را در نقطهای با دقت خواسته شده پیدا کنید. تنها چیزی که میتوان گفت این است که در نزدیکی $x=0$ به تعداد جملههای کمتری نیاز دارید و هر چه از آن دورتر و به مجانبهای عمودی نزدیکتر میشوید به تعداد جملههای بیشتری نیاز خواهید داشت. برای نمونه مقدار تابع در نقطهٔ $x=\frac{\pi}{4}$ تقریبا برابر است با $0.6019721029$ و با داشتن بسط تیلور بالا تا جملهٔ توان نهم به تقریبِ $0.6010920964$ میرسید که تا ۲-۳ رقم اعشار یکسان است. اما برای مقدار تابع در نقطهٔ $x=\frac{\pi}{2}-\frac{1}{10}$ مقدار تابع تقریبا برابر با $7.540498690$ است که حتی با داشتن بسط تیلور بالا تا جملهٔ توان چهلونهم به تقریب $7.494998012$ که تا ۰-۱ رقم اعشار یکسان است!