تابع $f(x)=\sin \frac 1x$ دارای دامنه $\mathbb R\setminus \{0\}$ است. در زیر می توانید شکل آن را ببینید. در نزدیکی صفر نوسان تابع بسیار شدید است:
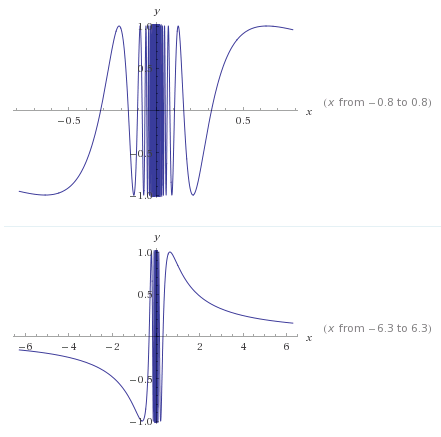
$\lim_{x\to 0}\sin\frac 1x$ وجود ندارد چون کافی است دو دنباله $a_n=\frac{1}{2n\pi}$ و $b_n=\frac{1}{2n\pi+\frac\pi2}$ را در نظر بگیرید و مشاهده کنید که $a_n\to 0,b_n\to 0$ ولی $\sin\frac1{a_n}\to 0$ و $\sin\frac1{b_n}\to 1$ . توجه کنید که چون $|\sin x|\leq 1$ لذا همواره برای هر تابع $f(x)$ هم داریم $|\sin f(x)|\leq 1$ پس در اینجا هم $|\sin\frac 1x|\leq 1$ .
تابع $x\sin \frac 1x$ دارای دامنه $\mathbb R\setminus \{0\}$ است. در زیر می توانید شکل آن را ببینید:
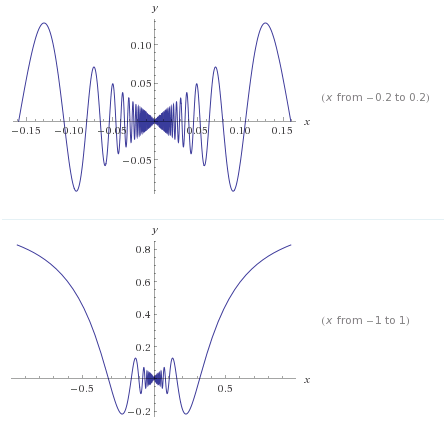
همان طور که مشاهده می کنید $\lim_{x\to 0} x\sin\frac 1x$ وجود دارد و برابر $0$ است یعنی $\lim_{x\to 0}x\sin\frac 1x=0$ . بدون استفاده از شکل هم این موضوع قابل حدس بود زیرا
$|x\sin\frac 1x|\leq |x|$ و از فشردگی استفاده کنید. اثبات این نامساوی هم واضح است چرا که گفتیم همواره $|\sin\frac 1x|\leq 1$ پس $|x\sin\frac 1x|=|x||\sin\frac 1x|\leq |x|\times 1=|x|$ . در زیر نمودارهای $y=x$ و $y=x\sin\frac1x$ مقایسه شده اند:
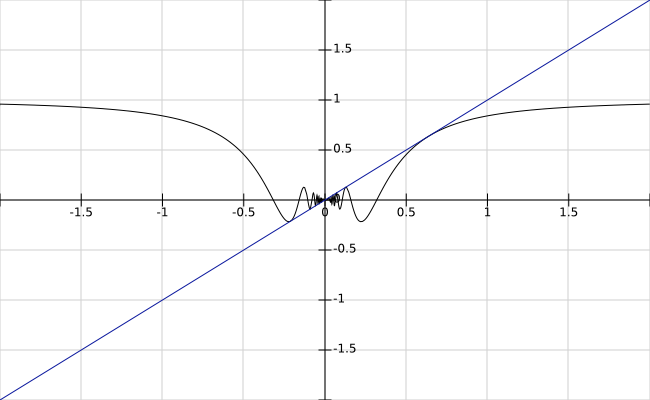
تابع $f(x)=x^2\sin\frac 1x$ هم دارای دامنه $\mathbb R\setminus \{0\}$ است. شکل آن به صورت زیر است:
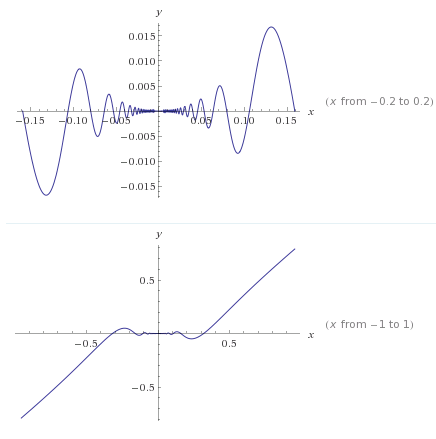
همانطور که میبینید سرعت همگرایی این تابع به سمت صفر بیشتر از سرعت همگرایی تابع قبلی به سمت صفر است. پس $\lim_{x\to 0}\ x^{2} sin\frac 1x=0$ . با استفاده از قضیه فشردگی هم این حد قابل انتظار بود.
در حالت کلی در توابع $y=x^n\sin\frac 1x$ که $n\in\mathbb N$ است داریم $\lim_{x\to 0}x^n\sin\frac 1x=0$ ولی حد $\lim_{x\to 0}\sin\frac 1x$ وجود ندارد!