مربعی به طول ضبع 1 را در نظر میگیریم و شکل زیر را طبق صورت مسئله در نظر میگیریم:
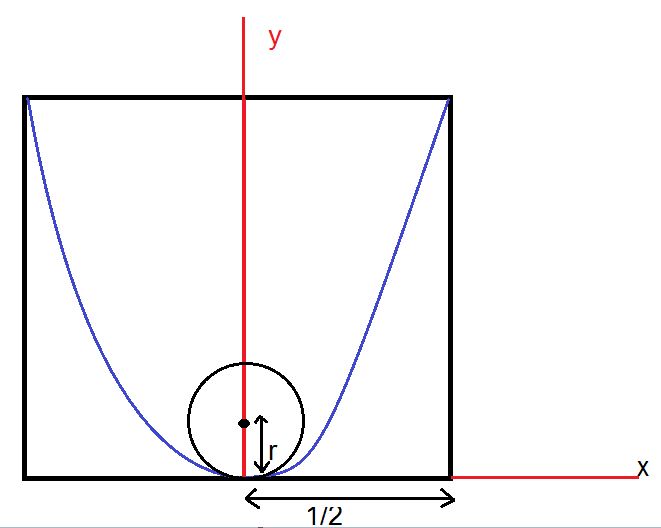
مطابق فرض مسئله، کانال به صورت سهمی است و مطابق شکل نقاط $(0,0), ( \frac{1}{2}, 1), (\frac{-1}{2}, 1) $ روی این سهمی قرار دارند. لذا اگر فرض کنیم که معادله سهمی به صورت
$$ y=a x^{2} $$
باشد آنگاه داریم:
$$ 1=a( \frac{1}{2})^{2} \longrightarrow a=4 $$
لذا معادله سهمی به صورت
$$y=4x^{2} $$
است. از طرفی دایره در مرکز بر این سهمی مماس است، پس معادله این دایره میتواند به صورت زیر باشد
$$ x^{2}+(y-r)^{2}=r^{2}$$
بنابراین با جایگذاری معادله اول در دوم داریم:
$$ \frac{y}{4} + y^{2}-2ry=0 $$
با مشتق گیری $ r$ بر حسب $ y $ داریم:
$$ \frac{dr}{dy}=0 \longrightarrow r=y+ \frac{1}{8} $$
لذا داریم:
$$\frac{y}{4} + y^{2}-2ry=\frac{y}{4} + y^{2}-2(y+ \frac{1}{8} )y=0 \longrightarrow y=0 \vee y= \frac{-1}{2} $$
$$ \Longrightarrow $$
$$r= \frac{1}{8} \vee r=- \frac{3}{8} $$
که دایره به شعاع $ r=-3/8$ خارج این سهمی است لذا ماکسیمم برابر با $r=1/8 $ است.