تابع $f(x)=x\sin\frac 1x$ در صفر تعریف نشده است. و در اطراف صفر هم نوسان دارد یعنی نه صعودی است و نه نزولی. در واقع برای هر $\epsilon> 0$ اگر بازه $(0, \epsilon)$ را در نظر بگیرید در اینصورت در این بازه می توان نقاطی مانند $x,y$ که $x< y$ را یافت به طوریکه $f(x)< f(y)$ و یا
$f(x)> f(y)$ به عنوان مثال بنابر اصل ارشمیدسی اعداد می توان $k$ طبیعی را چنان یافت که
$\frac 1{2k\pi},\frac1{2k\pi+\frac\pi2},\frac1{2k\pi+\pi}< \epsilon$ و $f(\frac 1{2k\pi})< f(\frac1{2k\pi+\frac\pi2})$ و $f(\frac1{2k\pi+\frac \pi2})> f(\frac1{2k\pi+\pi})$
چون در صفر تعریف نشده است اصلا در تعریف اکسترمم نسبی نمی گنجد در واقع این نقطه در دامنه نیست که حالا ماکسیمم یا مینیمم نسبی شود یا نه.
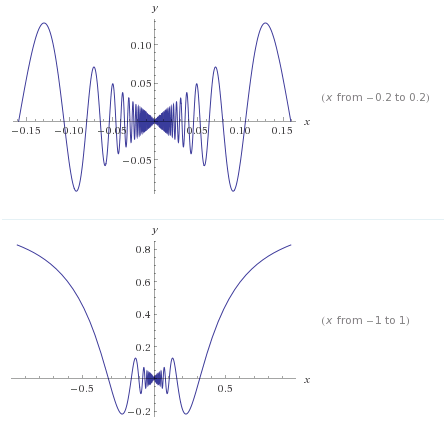
شکل آن به صورت زیر است: