ШЁЩҶШ§Щ… Ш®ШҜШ§. Ш·ШЁЩӮ ШҙЪ©Щ„ ШӯШ¬Щ… ШӯШ§ШөЩ„ Ш§ШІ ШҜЩҲШұШ§ЩҶ ЩҶЫҢЩ… ШҜШ§ЫҢШұЩҮ ШӯЩҲЩ„ Щ…ШӯЩҲШұ $x$ЩҮШ§ ШҜШ§ШұЫҢЩ…:
$$V= \int \pi y^2dx= \int _{-3}^{3} \pi y^2dx=2 \pi \int _{0}^{3}y^2dx$$
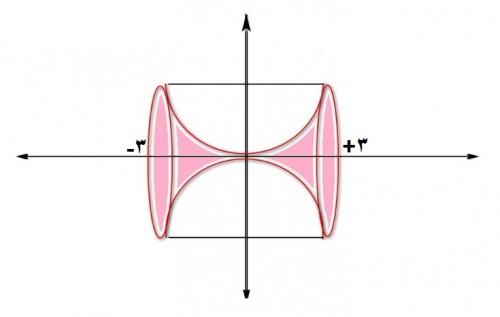
ШҜШұ Ш§ЫҢЩҶ ЩҒШұЩ…ЩҲЩ„ Щ…ЩӮШҜШ§Шұ $y$ Щ…Ш№Ш§ШҜЩ„ЩҮ ЩҶЫҢЩ… ШҜШ§ЫҢШұЩҮ Ш§ШіШӘ. Ш§ШЁШӘШҜШ§ Щ…Ш№Ш§ШҜЩ„ЩҮ ШҜШ§ЫҢШұЩҮ ШЁШ§Щ„Ш§ЫҢ Щ…ШӯЩҲШұ $x$ЩҮШ§ ШұШ§ ШЁШҜШіШӘ Щ…ЫҢвҖҢШўЩҲШұЫҢЩ… ШіЩҫШі ШЁШұШ§ЫҢ $y$ ШҜЩҲ Щ…ЩӮШҜШ§Шұ ШЁШҜШіШӘ Щ…ЫҢвҖҢШўЫҢШҜ Ъ©ЩҮ ЫҢЪ© Щ…ЩӮШҜШ§Шұ ШўЩҶ Ш¬ЩҲШ§ШЁ Ш§ШіШӘ.
$$x^2+(y-3)^2=9 \Rightarrow(y-3)^2=9-x^2 \Rightarrow y-3= \pm \sqrt{9-x^2} \Rightarrow y=- \sqrt{9-x^2} +3 $$
$$V=2 \pi \int _{0}^{3}y^2dx=2 \pi \int _{0}^{3}(3- \sqrt{9-x^2} )^2dx=2 \pi \int _{0}^{3}(9+9-x^2-6\sqrt{9-x^2})dx$$
$$V=2 \pi \int _{0}^{3}(18-x^2-6 \sqrt{9-x^2} )dx$$
$$ \bbox[5px,border:2px solid red]
{
\int ( \sqrt{a^2-x^2} )dx= \frac{x}{2} \sqrt{a^2-x^2} + \frac{a^2}{2} \arcsin (\frac{x}{a})
}
$$
$$V=2 \pi \big[18x- \frac{x^3}{3}-3x \sqrt{9-x^2}- 27\arcsin (\frac{x}{3}) \big] _{0}^{3}=90\pi-27\pi^2 $$